Control Index
Control System Block Manipulation
The table below relates the control block symbols to the control equation and also illustrates how changes in the control block arrangements can be changed whilst retaining the original control function.
| Block Operation | Original Arrangement | Modified Arrangement | Equation |
| Blocks In Series | 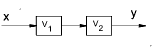 |
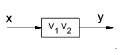 |
y = V1.V2.x |
| Blocks in Parallel | 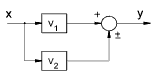 |
 |
y = (V1 ± V2) . x |
| Blocks in Feedback Loop | 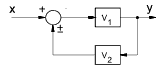 |
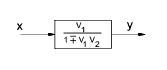 |
y = V1( x ± y . V2) or y = [ V1 / (1 |
| Moving a Summing Block Ahead of an element |
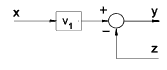 |
 |
y = V1.x - z |
| Moving a Summing Block beyond of an element |
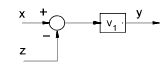 |
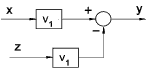 |
y = V1.(x - z) |
| Moving an take-off point ahead of an element |
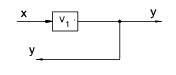 |
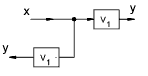 |
y = V1. x |
| Moving an take-off point beyond an element |
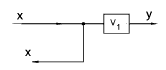 |
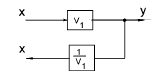 |
y = V1. x |
| Removing an element from a forward path |
 |
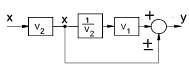 |
y = x. ( V1 ± V2 ) |
| Inserting an element in a forward path |
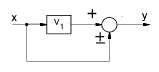 |
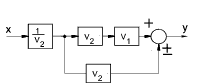 |
y = V1. x ± x |
| Removing an element from a feedback path |
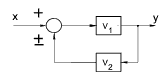 |
 |
y = V1( x ± y . V2) or y = [ V1 / (1 |
| Inserting an element in a feedback path |
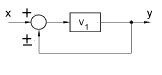 |
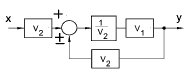 |
y = V1( x ± y ) or y = [ V1 / (1 |
| Rearrangement of summing points |
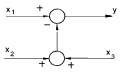 |
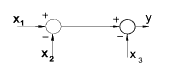 |
y = x1 - x2 - x3 |
| Interchange of summing points |
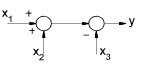 |
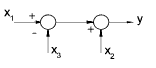 |
y = x1 + x2 - x3 |
| Moving a Take-off point ahead of a summing point |
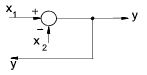 |
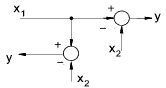 |
y = x1 - x2 |
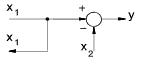
| Moving a Take-off point beyond a summing point |
 |
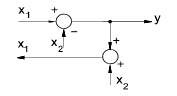 |
y = x1 - x2 x1 = y + x2 |
Sites & Links For Control Information
|
|
Control Index