Introduction
This page contains outline notes on thermal effects associated with electricity. The notes include
the Seebeck Effect, The Peltier Efffect and the Thomson Effect. The notes are outline in
nature to provide basic understanding of the principles for mechanical engineers.
The Effect of Temperature on Resistance
The resistance of metals increases with the temperature in accordance
with the formula>
R = Rref ( 1 + ρ(t-tref))
R = resistance at temperature t. R ref = resistivity
at temperature t ref C and ρ is the temperature
coefficient of resistance.
Table of Resistance in Ohms per m cube and Temp coefficents C-(per cent)
Note: The Resistivity is effectively Ohms . m2 /m length and therefore has the units of Ohms.m..
Example:A 10 m long length of iron of csa = 0,1 mm2 with a specific resistance of 90.10-9ohm.m has a resistance of
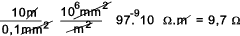
| Metal | Ro @ 0 deg C | ρ (0-100oC) |
| (x 10-9)Ohms. m | C (x 10-3) |
| Aluminium | 26,65 | 4,35 |
| Antimony | 41,8 | 3,9 |
| Bismuth | 1110 | 3,5 |
| Brass (58% Cu) | 59 | 1,5 |
| Brass (63% Cu) | 71 | 1,5 |
| Copper | 16 | 4,26 |
| Gold | 22 | 3,77 |
| Iron | 97 | 6,25 |
| Lead | 206 | 4,11 |
| Mercury | 940,7 | 0,72 |
| Nickel 200 | 9,5 | 6,2 |
| Platinum- | 109 | 3,67 |
| Silver | 16 | 4,0 |
| Tin | 110 | 4,4 |
| Tungsten | 55 | 4,6 |
| Zinc | 59 | 4,1 |
| Constantan | 490 | +/- 0,02 |
| Manganin | 467 | 0,015 |
| Nichrome | 1100 | 0,43 |
Important Note: In completing this table I have used a number of reference sources. The values
provided by these sources varies a little for each element. I could have shown a range for each
element /alloy but I decided to show typical values. If accurate values are needed please
consult more reliable references . (see links below)
The Seebeck Effect
When two wires of different materials are joined together to make a complete circuit and one
of the junctions is heated then a current will flow as shown. This effect is called the Seebeck effect
after the discoverer Thomas Seebeck...
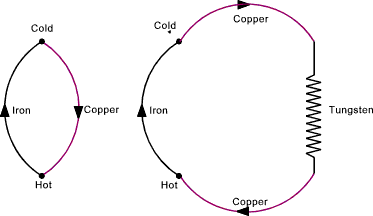
The arrangement is called a thermocouple. The value of the e.m.f generating this current
(Seebeck current) is dependent on the following:
a) The materials of the hot and cold junction
b) The temperature of the cold junction
c) The difference in temperature of the junctions
If a third material conductor is linked into one of the thermocouple
components, as shown, the overall thermocouple effect is not changed.
The e.m.f /temperature relationship is as shown below
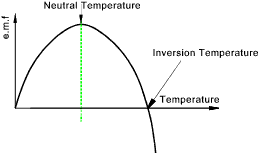
The relationship can be approximately represented by the formula
E = At + Bt2
The main applications which utilise this effect involve the use of semiconductors which
provide by far the greatest e.m.f's in relation to the thermal gradients.
A and B are constants
The Peltier Effect
When a current flows around a circuit made up of two dissimilar metals heat is absorbed
at one junction and is rejected from the other. This effect is shown in the figure below:
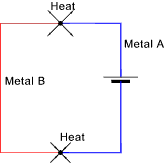
The effect is completely reversible in that if the e.m.f. is reversed the emmitting junction
will become the absorbing junction and the absorbing junction will become the radiating junction.
The rate at which the heat is absorbed or radiated is proportional to the current. The effect is not
related to that resulting from heating due to current flow through a resistance. Heating due to
conductor resistance is not reversible and is proportional to the square of the current.
The accepted explanation of this effect is that at the junctions e.m.f.s exist. One e.m.f is aiding the source
e.m.f. and contributes energy to it (it loses some energy and cools) the other
e.m.f. is driving against the source e.m.f and radiates energy. (it acts like a resistance and it heats)
The peltier e.m.f. is proportional to the absolute temperature and depends on the metals in the circuit. Its magnitude
is less than the Seebeck e.m.f to which it contributes.
The main applications which utilise this effect involve the use of semiconductors which
provide by far the greatest thermal gradients in relation to the current flows.
The Thomson Effect
It has been proved that the total Seebeck effect is due to the sum of the Peltier effect and the
Thomson effect.
The Thomson effect was discovered by William Thomson (Lord Kelvin) and is an e.m.f which depends only
on the temperature gradients in the metals . This e.m.f is such, that current flowing
through an unequally heated conductor absorbs heat if it flows from the cold end to the hot end,
and gives out heat if it flow the other way.
The thomson effect is only of significance if there is current flow and an
temperature gradient at the same time.
So far the Thomson effect does not seem to be of technical importance
|