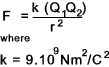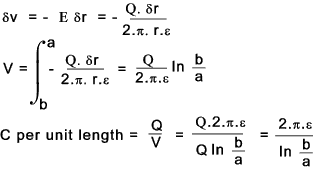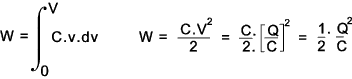Introduction
Electrostatics is the study of the electrical fields surrounding electrical charges and the resulting forces
between charged surfaces. The resulting interactions are entirely dependent on the
charges and their relative positions and not by their motion.
Two glass rods rubbed with silk, become charged with static electricity, and repel each other and
two ebonite rods rubbed with fur, become charged with static electricity, and repel each other.
However the charged glass rods attract the charged ebonite rods . It has been accepted
by convention that the glass rods have become positively charged and the ebonite rods have
become negatively charged. The processes result in the silk acquiring a negative
charge and the fur acquiring a positive charges.
A positive charge means that the object has lost electrons and is no longer electrically
neutral. Each electron lost results in an increase of charge of +1.6 x 10-19
coulombs. Since electric charge is conserved, the system (glass rod and silk together) maintains a net charge of 0.
A negative charge means that the object has gained electrons. Each electron
gained results in a charge change of -1.6 x 10-19 coulombs.
The following list shows part of the tribo-electric sequence.
When any two substances shown in this list are rubbed together, the top one will become
positively charged while the lower one will become negatively charged.
The further apart the two substances are in the list, the greater the electrification.
- ++
- Asbestos
- Fur (rabbit)
- Glass
- Mica
- Wool
- Quartz
- Fur (cat)
- Lead
- Silk
- Human skin, Aluminum
- Cotton
- Wood
- Amber
- Copper, Brass
- Rubber
- Sulfur
- Celluloid
- India rubber
- --
|
Nomenclature
C = Capacitance (farads)
D = electric flux density ( coulombs/m 2)
Ε = Field Strength (volt/m)
d = Dielectric thickness (m)
F = force (newtons)
Q = Charge (coulombs)
Q = Flux (coulombs)
V = e.m.f. or potential difference (volt)
ε o = permittivity of free space (farad /m = F/m)
ε r = relative permittivity
ε = absolute permittivity =ε o.εr..(farad /m = F/m)
Gold Leaf Electroscope
An electroscope is a device to determine or measure
the presence of electrostatic charges. The device's operation is simply
based on the Coulomb Force Law. This is a relatively crude instrument used
only for education. Modern instruments, based on vacuum tubes or solid state
technology can be used to measure extremely small charge levels.
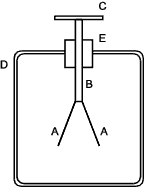
Two gold leafs (A) hang from a metal rod (B) within a metal container D.
The top of the rod supports a conducting disc C (or a sphere). The rod is
supported in a highly insulating stopper (E).
If the gold leaves become charged, because each leaf
is equally charged , the leaves repel each other.
The metal case isolates
the gold leaves from external influences. The case includes a window to
enable the leaves to be viewed.
The electroscope is very useful for illustrating two methods of transferring electrical charges: induction and
conduction. The two figures below show the principles in action.
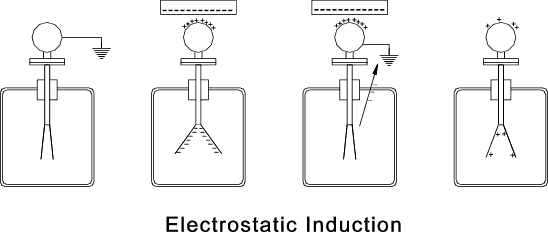
First the electroscope is earthed. A negatively charged object is moved close to
the electroscope system causing a separation of charges the -positive charges moving towards the charged objects and negative charges moving to the
gold leaves causing them to separate. If the electroscope is earthed without moving the charged objects
then the negatively charges flow to earth. If the earth and the charged objects are removed the positive charges
distribute over the electroscope system...
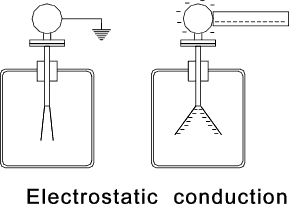
Physical contact by a charged object causes a flow of charge into the electroscope. This is used to
identify that the object is charged.
Electric Field
A charged point is surrounded by an electric field which are effectively lines of force radiating
outwards. The conventional direction assumed for these lines of force are from positive charge
to negative.i.e the lines indicate the force experienced by a positive charge . The lines
of force never intersect and therefore any charge will experience a force in one direction at any location.
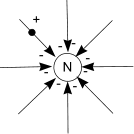
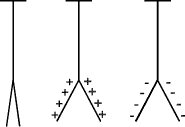
Lines of force associated with
negatively charged point
The forces of attraction and repulsion acting on adjacent charges will cause a
charged surface to be evenly distributed with lines of force radiating
outwards as shown in the two examples below
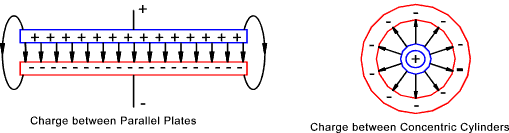
If the space between the surface allows any sort of conduction the charges will tend to
migrate across the space and neutralise itself.
The potential to which a body is raised by an electric charge is proportional to the
charge of the body - so V= k.Q where V is the voltage in volts , k = a constant called the capacity, and
Q is the charge in coulombs. The unit of potential is the work done in joules to
bring a unit charge (1 coulomb) from infinity to a point at unit potential.
The actual measure of capacity is termed capacitance and for practicality its units
are arranged using volts and coulombs. The unit of capacity is the farad .
The farad is the capacitance in which 1 coulomb is stored for a potential difference of 1 volt.
C = Q/V... or Q = CV
The strength of the force experienced by a unit charge in a field is called the field
strength (also called the electric stress) . This is measured in
newtons per unit charge and is represented by Ε
If there is a potential difference of 1V between two large plates separated by a vacuum of thickness d. The work required
to transfer a charge of 1 coulomb from one plate to the other is V joules. Work done is force time distance and therefore
the force experienced by the charge in the electric field is
Ε = V /d volts per metre
The lines of electrical force are called the flux of the system .
The flux is measured in coulombs i.e a charge of
Q coulomb creates a flux of Q coulomb. The flux passing through a unit area is called the flux
density D
D = Q /A coulombs per metre 2
The permittivity of free space in a vacuum is the ratio of
flux density to the electric field strength and is easily obtained as follows
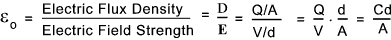
If the material between the plates is not a vacuum then the ratio
( D / E)is is different to the permittivity of
free space and is generally identified as ε ( absolute permittivity).
The absolute permittivity equals ε o.ε r
where ε r is the relative permittivity.
Different values of relative permittivity are tabled at the bottom of this page...
Coulomb Force Law
All bodies are able to take a charge of electricity and this is termed static electricity. The charge on a body
is measure by means of the force between the charges.
The Coulomb force law, which only applies to charged points, is stated below..
The force of attraction or repulsion between two charged points is directly proportional to the charges and inversely proportional to the square of the distance between them.
If the space between the charges is not a vacuum or air the law may be written
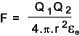
Note: a negative force results if the points have opposite charges and a positive
force results if the points have the same polarity
F = Force between points (N) -ve = attraction and +ve = repulsion
εo permittivity of free space.. ....Note: The value of εo is 8,85x 10 -12 F/m
Q1, Q2 = Charges on point 1 and point 2 (Coulomb)
r = radial separation on points (m)
The above equation can be simplified as follows.
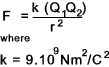
If the space between the charges is another material or air the law may be written
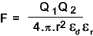
εr relative permittivity of material.
The value of k will also be different if the separating medium is not a vacuum or air.
Capacitance
A physical capacitance is often made up of plates insulated from each other by
insulating materials selected to be able to withstand high voltages. This insulating material is called the
dielectric. The capacitance is directly related to the permittivy of the dielectric and the area of the plate
and is inversely related to the distance between the plates.
The rating of a plate capacitance is given below
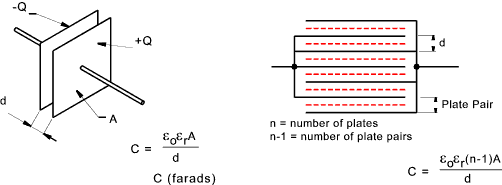
If the capacitor is a multi-plate type then the capacitance is simply the capacitance of one plate multiplied by
the number of paired plate faces. i.e a n plate unit would have capacitance of a two plate unit x (n-1)...
If there are two layers of dielectric between the plates, the capacitor is called a composite
capacitor and behaves as two capacitors in series with the individual and total capacitances as follows:
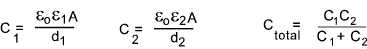
The capacitance of two co-axial cylinders is calculated as follows.
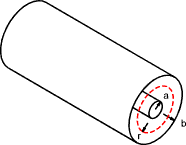
Let Q be the charge per unit length of cylinder.
The flux density/unit length at any radius D= Q / ( 2.π.r )
The electric field E = Q / ( 2.π.r.ε ) . ........ ε = εo.εr
δv is the voltage change between r and r + δ therefore δv = - E.δr
The total voltage between the conductor is
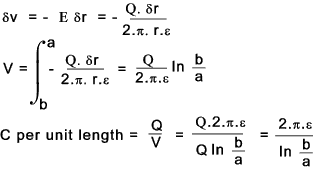
Energy stored in a Capacitance
Assume there is a p.d. across a capacitance of C farads which is increased
from v to v + δv
The charging current i = C. dv/dt
The instantaneous power to the capacitor = i.v (watts) = v.C dv /dt watts
The energy supplied in time dt = ( v.C dv/dt).dt = vc.dv joules.
The total energy supplied to the capacitor when the p.d is increased for 0 to V =
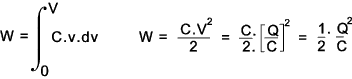
The energy per cubic metre for a capacitor with an plate area A and a dielectric thickness d =
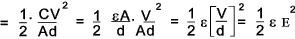
Therefore
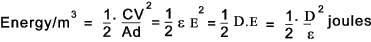
Force of attraction between oppositely charged plates
Consider two plates are separated by distance x in a medium of absolute permittivity ε
each plate having an area A.
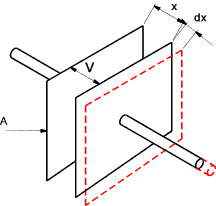
If the p.d between the plates is V then from the equation above
the energy per cubic metre of dielectric =
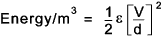
Assume one of the plates is movable as shown .
The force of attraction between the plates is F (newtons) .
Disconnect the plates from the supply.
The movable plate is moved out by dx
Assume there is no leakage through the dielectric and therefore charge on the plates remains constant.
Therefore the electric flux density and the potential gradient through the dielectric remains stays the same
The energy per cubic metre is unchanged.
Therefore as the volume is increased by Adx the energy must increase also
This energy must be derived from the work done in moving the plate.
The work done in moving the plate = F.dx joules .
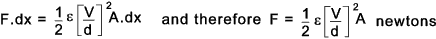
The force of attraction between the plates is 0,5.ε.A .(Voltage Gradient)2
Dielectric Strength
The dielectric material can withstand a certain potential difference. If the pd is increase
above this value there is a high risk that it will break down. This potential difference is called the dielectric strength.
Capacitors made with high dielectric strength materials can have higher capacity because the dielectrics can have
lower thickness for the same voltage rating. Typical dielectric strenth values are provided below..
| | | |
| Material | Thickness .....
mm | Dielectric Strength
MV/m |
| Air (NTP) | 0,2 | 5,75 |
| Air (NTP) | 1,0 | 4,46 |
| Air (NTP) | 6,0 | 3,27 |
| Air (NTP) | 10 | 2,98 |
| Mica | 0,01 | 200 |
| Mica | 0,1 | 176 |
| Mica | 1 | 61 |
| Glass | 1 | 28,5 |
| Glass | 5 | 18,3 |
| Ebonite | 1 | 50 |
| Paraffin - Waxed Paper | 0,1 | 40-60 |
Table show relative permittivity for different materials
Note: the permittivity of some materials varies with the frequency of the applied voltage.
| Material | Relative
permittivity εo |
Material | Relative
permittivity εo |
Material | Relative
permittivity εo |
| Air | 1,006 | Nylon | 5 | Slate | 4 |
| Araldite | 3,6 | Oil Paper | 4 | Soft Rubber | 2,5 |
| Bakelite | 3,6 | Olive oil | 3 | Steatite | 6 |
| Castor oil | 4,7 | Paper | 2,3 | Sulfur | 3,5 |
| Ebonite | 2,5 | Paper impregnated | 5 | Teflon | 2 |
| Glass | 5 | Parafin oil | 2,2 | Turpentine | 2,2 |
| Guttapercha | 4 | Polythene | 2,3 | Transformer oil (mineral | 2,5 |
Hard paper
laminated | 4,5 | Petroleum | 2,2 | Vulcanite | 80 |
Insulation
H.V.cables | 4,2 | Phenolic resin | 8 | Vacuum | 1,000 |
Insulation
Telephone.cables | 1,5 | Plexi glass | 3,2 | - | - |
| Marble | 8 | Porcelain | 6 - 7 | | - |
| Mica | 3 - 7 | Quartz | 4,5 | - | - |
| Micanite | 6 | Shellac | 3,2 | - | - |
Comparison of Electromagnetic and Electrostatic Variable names and Symbols
| | | |
| Electrostatics | Electromagnetics |
| Names | Symbol | Name | Symbol |
| Electric flux | Q | Magnetic flux | Φ |
| Electric flux density | D | Magnetic flux density | B |
| Electric field strength | E | Magnetic field strength | H |
| Electromotive force | E | Magnetomotive Force | F |
| Electric potential difference | V | Magnetic potential difference | - |
| Permittivity of free Space | εo | Permeability of free space | μo |
| Relative permittivity | εr | Relative permeability | μ |
| Absolute permittivity | D/E | Absolute permeability | B/H |
|