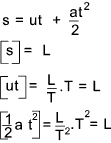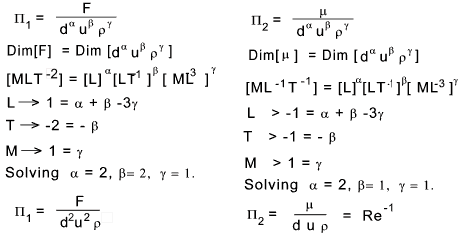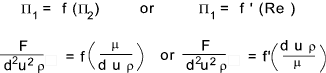Introduction
Many physical relationships in engineering and especially in
fluid mechanics are, by nature, extremely complex.
Often a phenomenon is too complicated to, theoretically, derive a formula
describing it e.g the forces experienced when an object moves through a fluid.
Dimensional analysis is then used to identify variables which can be
combined in groups which are definitely related. Experiments can then be
completed to formulate this relationship and allow determination of the actual
performance characteristics of real world systems..
This method derives from the principle that each term in an equation
depicting a physical relationship must have the same dimension.
Non-dimensional quantities expressing the relationship among
the variables are constructed e.g. [Length / (Velocity.Time)], or [ Force / (Mass /Acceleration)].
These are equated and then experiments are complete to determine their
functional relationship.
The principles of dimensional analysis are developed from the
principle of dimensional homogeneity which is self evident.
It is characteristic of physical equations that only like quantities, that
is those systems having the same dimensions, are added or equated.
It is OK to to equate forces. ( 5 newtons = 2 newtons + 3 newtons.)
It is clearly not OK to equate forces with lengths ( 5 newtons = 2 newtons + 3 m)
Quantities Symbols and Dimensions
| Quantity | Symbol | Dimensions | |
Quantity | Symbol | Dimensions |
| Mass | m | M |
Mass /Unit Area | m/A 2 | ML -2 |
| Length | l | L |
Mass moment | ml | ML |
| Time | t | T |
Moment of Inertia | I | ML 2 |
| Temperature | T | θ |
- | - | - |
| Velocity | u | LT -1 |
Pressure /Stress | p /σ | ML -1T -2 |
| Acceleration | a | LT -2 |
Strain | τ | M 0L 0T 0 |
| Momentum/Impulse | mv | MLT -1 |
Elastic Modulus | E | ML -1T -2 |
| Force | F | MLT -2 |
Flexural Rigidity | EI | ML 3T -2 |
| Energy - Work | W | ML 2T -2 |
Shear Modulus | G | ML -1T -2 |
| Power | P | ML 2T -3 |
Torsional rigidity | GJ | ML 3T -2 |
| Moment of Force | M | ML 2T -2 |
Stiffness | k | MT -2 |
| Angular momentum | - | ML 2T -1 |
Angular stiffness | T/η | ML 2T -2 |
| Angle | η | M 0L 0T 0 |
Flexibiity | 1/k | M -1T 2 |
| Angular Velocity | ω | T -1 |
Vorticity | - | T -1 |
| Angular acceleration | α | T -2 |
Circulation | - | L 2T -1 |
| Area | A | L 2 |
Viscosity | μ | ML -1T -1 |
| Volume | V | L 3 |
Kinematic Viscosity | τ | L 2T -1 |
| First Moment of Area | Ar | L 3 |
Diffusivity | - | L 2T -1 |
| Second Moment of Area | I | L 4 |
Friction coefficient | f /μ | M 0L 0T 0 |
| Density | ρ | ML -3 |
Restitution coefficient | | M 0L 0T 0 |
Specific heat-
Constant Pressure | C p | L 2 T -2 θ -1 |
Specific heat-
Constant volume | C v | L 2 T -2 θ -1 |
Note: a is identified as the local sonic velocity, with dimensions L .T -1
Types of Similarity.
In order that the relationships determined for a model can be applied
to a real life application (prototype) there has to be a physical similarity between
the parameters involved in each one. The two systems are said to be physically similar in respect to specified
physical quantities when the ratio of the corresponding magnitudes of these quantities between the
two systems is everywhere the same. Within the general term physical similarity there
are a number of types of similarity some of which are listed below.
Geometric similarity... This is basically the similarity
of shape. Any length of one system is related to that of another system
by a ratio which is normally called the scale. All parts of the scale
model of a car should be in direct scale to the full scale
item if it is truly geometrically similar. This should ideally include such features as the
surface roughness. This does not include non dimensional features e.g. weight...
Kinematic Similarity... This is basically the similarity of motion and
implies that the geometric similarity and similarity of time intervals. i.e
ratios of length are fixed (r l) and ratios of time intervals
(r t) are fixed. The velocities (ds/dt) of corresponding parts should also
be in fixed ratios ( r l / r t ) and the ratios of
acceleration (dv/dt) are in ratios ( r l / r t 2 ).
Dynamic Similarity.. This is the similarity of forces. The magnitude of forces at
two similarly located points are in a fixed ratio. For systems involving fluids
the forces may be due to viscosity, gravitation, pressure, inertia, surface tension, elasticity etc etc... It is generally
accepted in fluid mechanics that the ratio of inertia forces is the most useful ratio.
Dynamic similarity involving flow with viscous forces...
The are numerous instances
of fluid flow affected only by viscous pressure and inertia forces.
A fluid flowing in a full pipe is such a case. For dynamic similarity
the ratio of magnitude of any two forces must be the same at corresponding points
(in a steady flow situation) . The ratio of inertia force
to net viscous force is chosen for review.
The inertia force is the mass x acceleration. [density (ρ ) x volume ( l 3 ) x acc'n ( u 2 / l )].
Note: The acceleration is chosen to be the characteristic velocity ( u ) divide by a particular time
interval ( l/ u ) = u 2 / l .
The magnitude of the inertia forces are therefore
proportional ( ρ.l 3 )( u 2 / l ) = ρ l 2 u 2
The magnitude of the shear stress resulting from viscosity is the product of the
viscosity (μ )and the rate of shear ( u / l ) acting over an area
proportional an area l 2 . This is therefore proportional to
( μ ) ( u / l ) x ( l 2 ) = ( μ u l )
The ratio of inertia forces to viscous forces is therefore as follows:
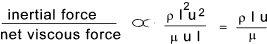
This ratio is very important in fluid mechanics, mainly for problems
involving flowing fluids, and it is called Reynolds number. The ratio for dynamic similarity between
two flows past geometrically similar boundaries and affected by only viscous and inertia forces is the same
if the fluids have the same reynolds number. In the UK for pipe flow
studies the characteristic length( l ) is the diameter ( D ) and the characteristic
velocity u is chosen as the mean velocity.
Dynamic similarity involving flow with gravity forces...
When considering forces with free
surfaces e.g. flows over weirs, channel flows, or surface motion around ships, the most significant
relationships is the ratio between the gravity forces and the inertia forces.
These are summerised below..
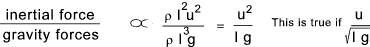
This ratio u /( lg ) 1/2 is called the Froude number .
Dynamic similarity exists between two flows which involve fluids
subject to only gravity and inertial forces if the Froude number , based on corresponding velocities
and lengths, is the same for both fluids...
The primary dimensionless groups in Fluid mechanics are listed below.
| Group | Name | Represents
Ratio of
Forces | Symbol |
| ρ l u / μ | Reynolds Number | Inertia / Viscous | Re |
| u / ( lg ) 1/2 | Froude Number | Inertia / Gravity | Fr |
| u / ( lρ / γ )1/2 | Weber Number | Inertia / Surface Tension | We |
| u / a | Mach Number | Inertia / Elastic | M |
Note: a is identified as the local sonic velocity, with dimensions L .T -1
Simple Example
Consider a body moving with constant acceleration. The relationship
is expressed as ..... s = ut + at 2 /2
Expressing this in terms of dimensions..
Note....[ z ] is used to say the dimensions of z
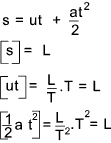
The above examples simply illustrates that the equation is dimensionally correct.
This exercise can be continued to produce a non-dimensional equation.
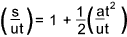
The terms within the brackets are non dimensional groups which can be considered a single variables
or groups. These are generally called denoted using the symbol Π the above equation
can be expressed as
Π 1 = 1 + Π 2..... or.....Π 1 = F [ Π 2]
There is no real advantage in using the principle for this simple example but for more complex
relationships the benefits can be significant.
Buckinghams Π theorem
Consider a physical phenomenon with an unknown defining equation.
First define what relationship is require. e.g The wind force experienced by a sphere
List the number of dependent variables and all relevant variables. eg F = f (d,u,ρ,μ )
Using base dimension (say L,M,T,η..F), set down the dimensions of all the variables.
e.g. F->[MLT-2] , d->[L] , u-> [LT-1] , ρ ->; [ML-3] ,
μ ->[ML-1 T-1]
Count the number of variables (n = 5) count the number of base dimensions used to
dimension the variables ( j = M,L,T).
note: For fluids j will generally = 3
Select j variables which include in their dimension which collectively include all
the base dimensions (in this case M,L & T].
e.g. Choose d->[L], u-> [LT-1], and ρ ->; [ML-3]
Form k dimensionless groups [k = n - j = 2]
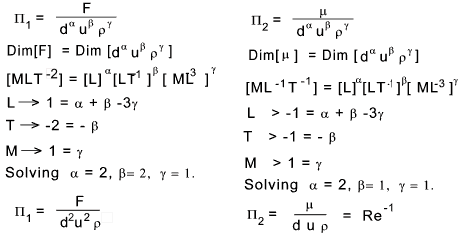
Use the resulting dimensionless groups to establish a relationship in which one group which includes
the dependent variable (F) as a function of the other groups..
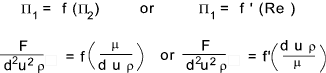
Buckinghams's theorem simply states that if there is a relationship
involving n variables and j base dimensions then k = n- j dimensionless groups ( Π groups )
can be created allowing physical relationships to be developed using experimental methods
|