Introduction
This page concerns fluid flows down channels and pipes which are not full. The fluid has a free surface
which is subject to atmospheric pressure. This naturally occurs with rivers, and canals, and drainage ditches. The notes also include
fluid flowing over weirs and notches.
Symbols
A = Area (m2)
F1 = Force of fluid down channel (N)
F2 = Force up fluid down channel (N)
g = acceleration due to gravity (m/s2 )
h = fluid head (m)
i = incline
l = length down slope (m)
lh = length --- horizontal (m)
m = wetted mean length (m)
p = fluid pressure (N /m2 )
p s= surface pressure (N /m2 )
P = perimeter (m)
ρ = fluid density (kg /m2 )
|
s wetted surface length (m)
u = velocity (m/s)
v = velocity (m/s)
x = depth of centroid (m)
θ =slope (radians)
ρ = density (kg/m3)
τ o = shear stress (N /m2)
|
Channel Flow
In an open channel, the flowing water has a free surface and flows by the
action of gravity. See figure below. The water flows with a velocity
v down a channel with an incline θ. The water depth is uniform and therefore
the downward force F1 is balanced by the upward force F2. The only force causing
motion is the weight component in the direction of motion ρgAl sin θ.
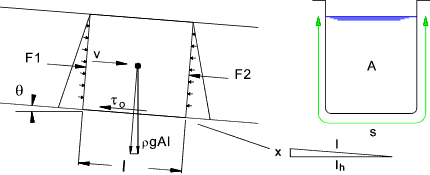
The fluid is not accelerating so the downward gravity force is balanced only by the
friction force between the fluid and the wall.
If the length of wetted perimeter = s and the shear stress at the wall = τ osl
ρgAl sin θ = τ osl
Now let the incline i be x / l h. For small angles i = sin θ .
ρgAli = τ osl ..
and therefore ..τ o = ρgAi / s
Now let m be the mean wetted depth (m = A/s) the resulting equation is .
τ o = ρgmi

Note: The relationship between τ o and f is proved at the bottom of this page..
The quantites 2g/f are combined as a single constant ( C2 ) yielding the equation known as Chezy 's formula
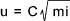
The value of C can be obtained using the Ganguillet---Kutter equation: with the relevant n values provided in the table below
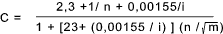
Mannings formula C = m1/6 /n also applies...Using the same tabled values of n
Table showing n coefficients for using in Mannings equation and Ganguillet---Kutter equation:
| | |
| Description |
n
Normal |
n
Range |
| |
|
|
| Glass |
0,010 |
0,009---0,013 |
| |
| Concrete |
| Culvert straight and free of debris |
0,011 |
0,010---0,013 |
| Culvert with bends, connections and some debris |
0,013 |
0,011---0,014 |
| Sewer with manholes, inlet etc straight |
0,015 |
0,013---0,017 |
| Unfinished steel form |
0,013 |
0,012---0,014 |
| Unfinished smooth wood form |
0,014 |
0,012 --- 0,016 |
| Finished wood form |
0,012 |
0,011---0,014 |
| |
| Clay |
| Drainage tile |
0,013 |
0,011---0,017 |
| Vitrified clay sewer |
0,014 |
0,011---0,017 |
| Vitrified clay sewer with manholes inlet etc |
0,015 |
0,013---0,017 |
| Vitrified sub drain with open joint |
0,016 |
0,014---0,018 |
| |
| Brickwork |
| Glazed |
0,013 |
0,011---0,015 |
| Lined with cement mortar |
0,015 |
0,012---0,017 |
| Sewer coated with slimes , with bends |
0,013 |
0,012---0,016 |
| Rubble masonary |
0,025 |
0,018---0,030 |
| |
| Cast Iron |
| Coated |
0,013 |
0,010---0,014 |
| Uncoated |
0,014 |
0,011---0,016 |
| |
| Excavated or Drained Channels |
| Earth after weathering ---straight or uniform |
0,022 |
0,018---0,025 |
| Gravel straight uniform |
0,025 |
0,022---0,030 |
| Earth winding clean |
0,025 |
0,023---0,030 |
| Earth with some grass, weeds |
0,030 |
0,025---0,033 |
| Earthe bottom rubble sides |
0,030 |
0,028---0,035 |
| Dragline excavated, no vegetation |
0,028 |
0,025---0,033 |
| Rock cut smooth uniform |
0,035 |
0,025---0,040 |
| Rock cut smooth irregular |
0,040 |
0,035---0,050 |
| Unmaintained channels dense weeds |
0,080 |
0,050---0,120 |
| |
| Natural streams |
| Clear straight, fullstage no rifts or deep pools |
0,030 |
0,025---0,033 |
| As above but with more stones and weeds |
0,035 |
0,030---0,040 |
| Clean, winding some pools and shoals |
0,040 |
0,035---0,045 |
| As above but some weeds and stones |
0,045 |
0,035---0,050 |
| |
| Flood Plains |
| Pasture short grass |
0,030 |
0,025---0,035 |
| Pasture high grass |
0,035 |
0,030---0,050 |
| |
| Cultivated Areas |
| No crop |
0,030 |
0,020---0,040 |
| Mature row crops |
0,035 |
0,025---0,045 |
| Mature field crops |
0,040 |
0,030---0,050 |
| |
| Major Streams Width > 30m |
| Regular section with no boulders or bush |
|
0,025---0,060 |
| Irregular and rough |
|
0,035---0,10 |
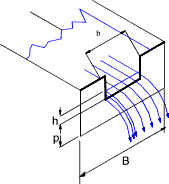
Thin Plate Weirs
1) Full Width Weir
Flow Q = 0,66√(2g). Cd b he 1,5
CD = 0,602 + 0,083 h/p
he = h + 0,0012m (h = measured head)
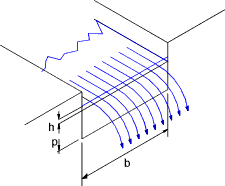
2) Supressed Weir
Flow Q = 0,66√(2g). Cd b. he 1,5
CD = 0,616(1 --- 0,1h/b)
he = h + 0,001 (h = measured head ---m)
3) Vee Notch Weir
Flow Q = (8/15)√(2g).Cd tan (θ /2 ). he 2,5
he = h + hk (h = measured head ---m)
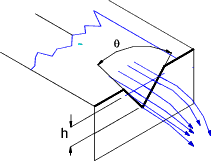
θ
Degrees |
Cd |
hk |
| 20 | 0,592 | 0,0027 |
| 40 | 0,581 | 0,0018 |
| 60 | 0,576 | 0,0011 |
| 80 | 0,578 | 0,0010 |
| 90 | 0,579 | 0,0009 |
Notes showing relationship between τo and f...Provided in support of proof of Chezy Formula above..
|
Showing relationship between τo and f
Darcy conducted experiments and proved that for pipes of uniform cross section and roughness and fully developed flow
the head loss due to friction (hf ) along a pipe is in accordance with the following formula.

The fluid shear stress (τ o ) at the boundary wall is related to the pressure differential along the pipe
by the expression.
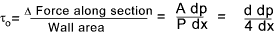
P = perimeter length, A = Area of section
The differential head along the pipe is related to the differential pressure as follows/
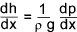
The equation for shear stress is modified as ..
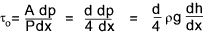
Now for fully developed flow with no axial sudden changes the flow pattern along the
pipe is constant and dh/dl is equal to h / l therefore ..
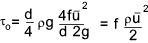
|
|