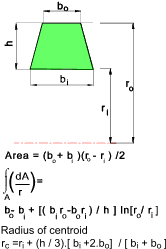
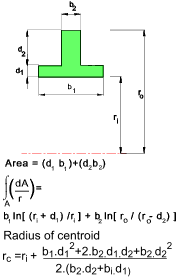
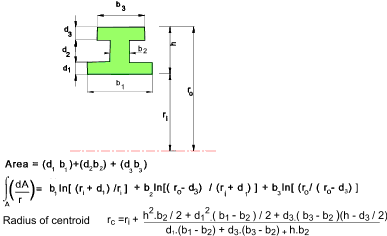
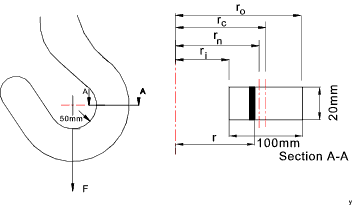
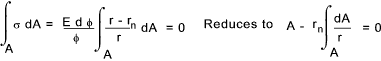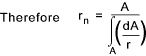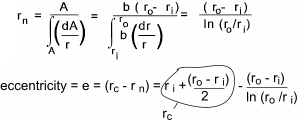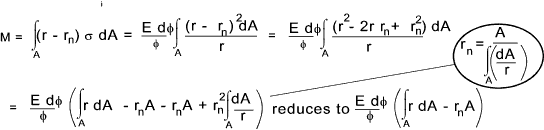Curved beams
|
Introduction The beam theory can also be applied to curved beams allowing the stress to be determined for shapes including crane hooks and rings. When the dimensions of the cross section are small compared to the radius of curvature of the longitudonal axis the bending theory can be relatively accurate. When this is not the case even using the modified Bernoulli-Euler only provides approximate solutions Symbols
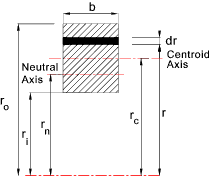
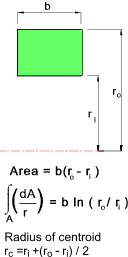
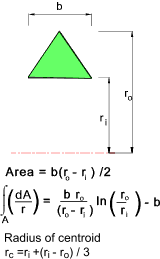
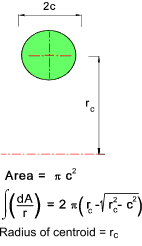
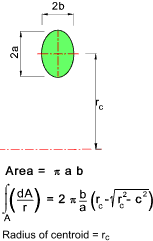
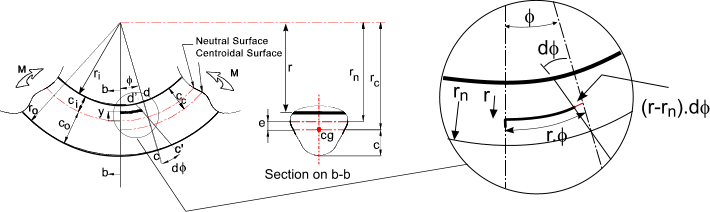
The sketch below shows a curved member subject to a bending moment M. The neutral axis
r n and the centroid r c are not the same.
The strain at a radius r =
The strain is clearly 0 when r = at the neutral axis and is maximum
when r = the outer radius of the beam (r = r o )
The location of the neutral axis is obtained from summing the product of the normal stress and the area elements over the whole area and equating to 0
Curved Beam in Bending The stress resulting from an applied bending moment is derived from the fact that the resisting moment is simple the integral over the whole section of the moment arm from the neutral axis (y) multiplied by σdA (= dF). Moment equilibrium is achieved if
The curved beam flexure formula is in reasonable agreement for beams with a ratio
of curvature to beam depth of rc/h of > 5 (rectangular section). As the
beam curvature/depth radius increases the difference between the maximum stress
calculated by curved beam formula and the normal beam formula reduces.
If the ratio is about 8 then a maximum stress error of only about 5% results from using the straight beam formulae. The hook is lifting a load of 25000N.
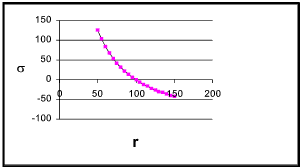
The stress values plotting against r are shown below:
The tensile stress at the inner surface is calculated at 126.76 N/mm2 and the compressive stress at the outer surface is calculated at -42,25 N/mm2...This section profile results in a tensile stress three times greater than the compressive stress. A more efficient section with the stresses balanced would result from having a wider inner section and a thinner outer section. | ||||||||||||
Sites Providing Relevant Information
|
|
 >
>