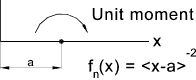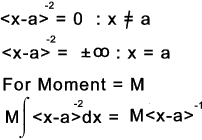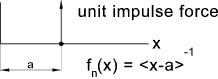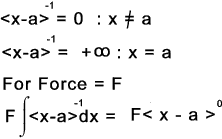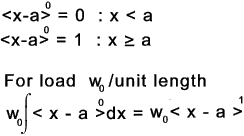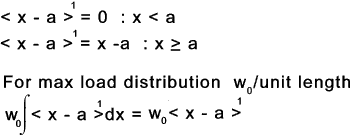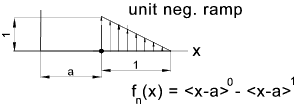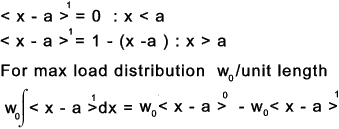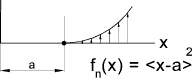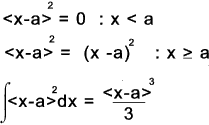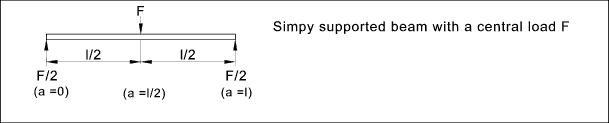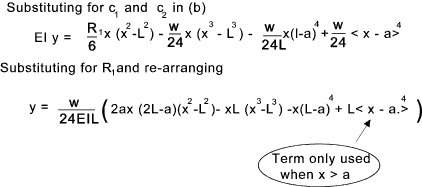Introduction
When calculating the shear Force and the bending moment diagrams for more complex loading
across discontinuities such as concentrated loads and moments. Simple methods are
not enough. For the more complicated cases the use of singularity functions provide
a convenient method.
A singularity function is expressed as
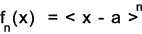
Where
n = any integer (positive or negative) including zero
a = distance on x axis along the beam,from the selected origin, identifying the location of the discontinuity.
Rules in applying singularity functions
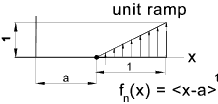
If n >0 and the expression inside the angular brackets is positive then
fn(x) = (x-a)n the expression is a normal algbraic formula
|
If n > 0 and the expression inside the angular brackets is negative then fn(x) = 0
|
If n < 0 then fn = 1 for x = a and fn(x) = 0 otherwise
|
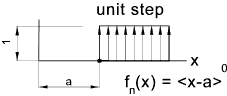
If n = 0 then fn = 1 for x >= a and fn(x) = 0 otherwise
|
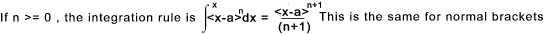 |
 |
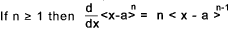 |
Unit Singularity
Function | Singularity Function as used |
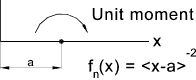 |
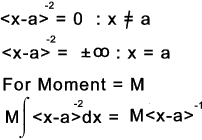 |
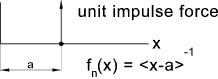 |
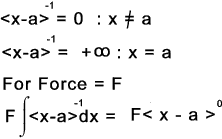 |
 |
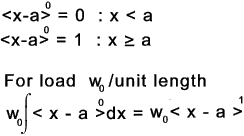 |
 |
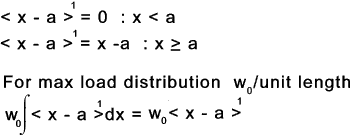 |
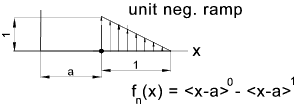 |
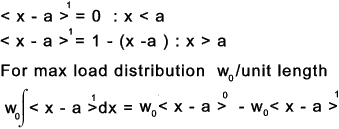 |
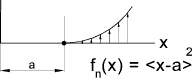 |
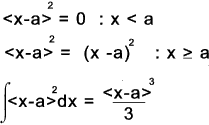 |
Example of using singularity functions for a simply supported beam
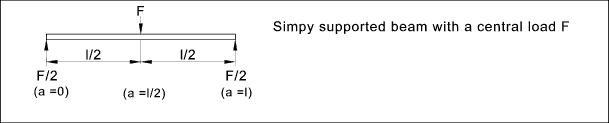

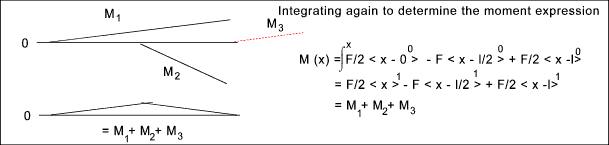
A more complex example of using singularity functions
The requirement is to obtain the Shear load, moment, slope and deflection anywhere along the beam as shown
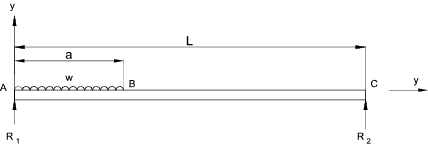



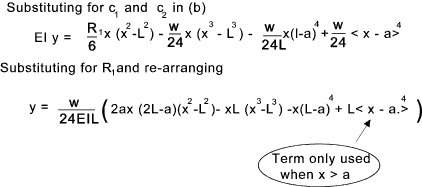
The equations above can be used to determine the shear load, moment, slope and deflection
for the beam from x = 0 to x = L
|