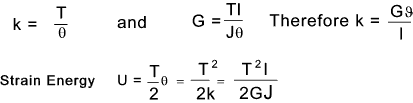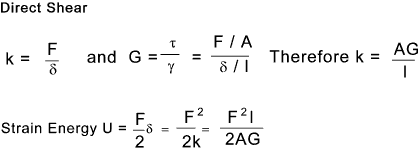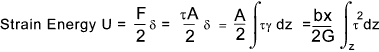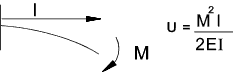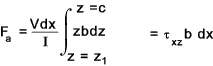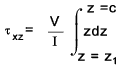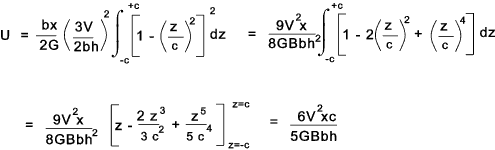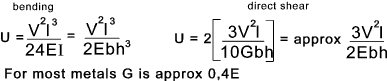|
Strain Energy
The external work done on an elastic member in causing it to distort
from its unstressed state is transformed into strain energy which is
a form of potential energy. The strain energy in the form of elastic
deformation is mostly recoverable in the form of mechanical work.
Nomenclature
c = distance from neutral axis to outer fibre(m)
E = Young's Modulus (N/m2)
F = Axial Force (N)
G = Modulus of Rigidity (N/m2)(m)
I = Moment of Inertia (m4)(m)
l = length (m)
M = moment (Nm)
V = Traverse Shear force Force (N)
x = distance from along beam (m)
z = distance from neutral (m)
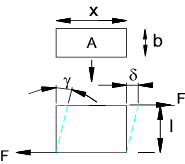
γ = Angular strain = δ/l
δ = deflection (m)
τ = shear stress (N/m2)
τ max = Max shear stress (N/m2)
θ = Deflection (radians)
Strain Energy Pure Tension and compression
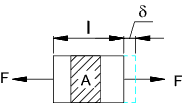

Strain Energy Pure Torsion
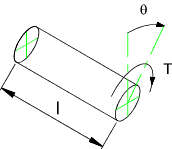
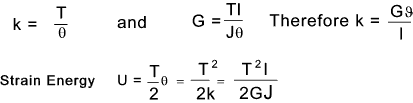
Strain Energy Direct Shear
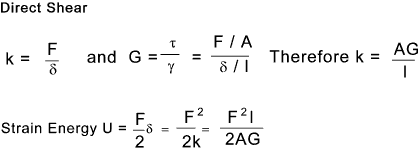
Alternatively allowing z to be a variable:..
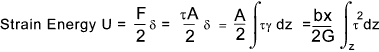
Strain Energy Beam in bending
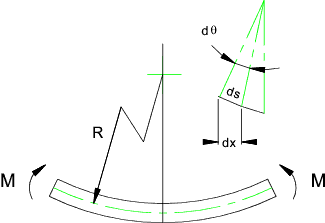

Illustrating the case when M is fixed and note related to x
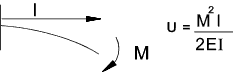
Illustrating the case when M is related, very simply to x
Strain Energy due to tranverse shear stress
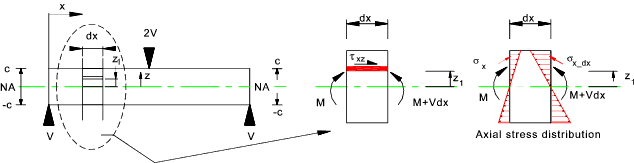
Consider a beam subject to traverse shear loading as shown. The beam is subject
to stresses as a result of bending moments. It is also subject to stresses as
a result of traverse shear load. These notes only relate to the stresses due
to the traverse shear load.
Consider the beam as shown and specifically a slice dx wide.
The beam width is b
There is a linear distribution of axial stress σx at a section at a distance x along the
beam =
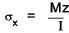
Along the slice dx the axial stress
increases to (M + Vdx)z/ I . Thus along the slice dx there is a increase
in axial stress of [(Vdx)z] / I.
The total increase in axial force over slice dx for the section of the beam from
z1 to the
outer fibre of the beam is balanced by a shear force = τ xz w dx as shown below.
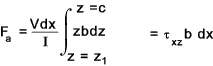
b is width: For a rectangle b = constant: For other section b may be a function of x
Solving for τ xz
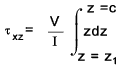
The maximum shear stress is at the neutral axis when z1 = 0 and the minimum shear stress is at
the outer fibre when z1 = c.
The equation for shear stress at any distance z from the neutral axis
for a rectangular suction, with
constant width b,subject to a traverse shear force V is as shown below.
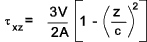
To obtain the strain energy substitute this equation into that derived for direct shear
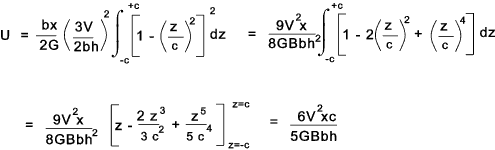
For the solid rectangle ( c = h/2, width = b, height = h, and length = x )subject to a
traverse force V load along its length the strain energy = ...
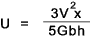
Using similar principles the strain energy for different sections subject to traverse
shear can be identified as shown below

Comparing the strain energy due to direct shear in a beam and that due to bending:
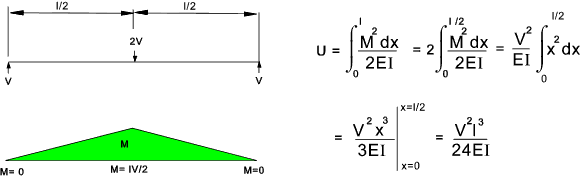
For the simply supported rectangular section beam with a central traverse force of 2V of length l the
strain energy due to bending and due to traverse shear as shown below.
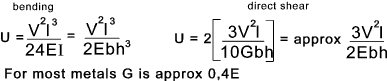
For a simply supported rectangular beam loaded, with single central load, The strain energy resulting
from the bending moments is [l2 /h2]/3 times that due to traverse shear loading.
For a typical beam of l/h ratio = 10 the bending shear energy is 33 times the traverse force shear energy. The traverse
force shear energy can be neglected for most beams of significant length.
Summary
The strain energy in a member or component for each type is loading is shown below:
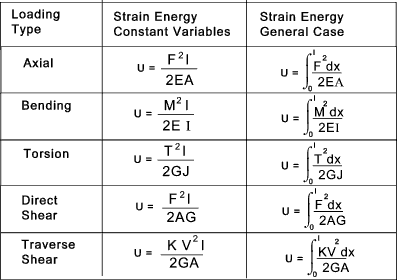
Note :The constant K for the traverse shear option is shown in the section on traverse
shear above. For a Structural section (K = 1)
|