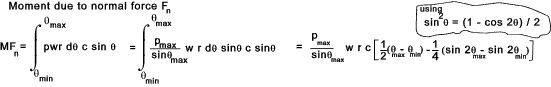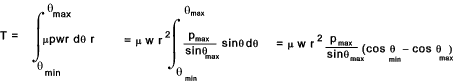Brakes
Block Brakes
Introduction This type of braking system has been generally used before the 1930's for transport systems
and machinery. It is a very simple concept and requires minimum engineering.
The brake has the disadvantage that the braking surfaces are open to the environment and are easily
contaminated. These brakes are often seen on steam traction engines, steam rollers, etc.
Nomenclature
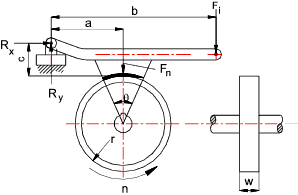
F = Applied Force (N) Short Block The maximum normal force applied by the block = F n = p max.r θ w The torque capacity of the brake = Tmax = Fn μ r
Taking moments about the lever pivot point, the maximum operating force = F i = Fn(b - μc) / a The system as drawn is to some extent self energising because the friction force
reduces the actuating force necessary. If the pivot point is located below the
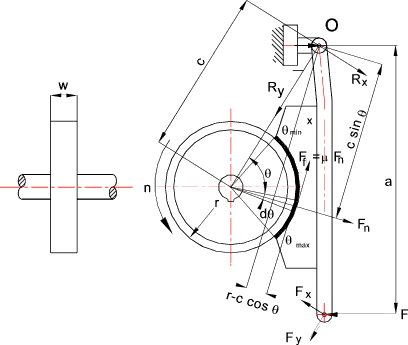
brake contact point the brake would not be self sustaining The long block pressure distribution calculation assumes that the lever arm is rigid and the pressure is directly related to the distance from the pivot point. The pressure is proportional to c sin θ or p = k sin θ where k is some constant. For a specific brake material the maximum pressure = pmax. k = p max /sin θ max... and...
p = sin θ(p max /sin θ max) The value of minimum θ is usually set to above 100 and the maximum pressure
when the value of sin θ is 900. above this angle the pressure reduces.
Therefore if the maximum value of θ is less than 900
the sin θ max = sin θ. if the maximum angle is greater than 900
then sin θ max = sin 900
To calculate the maximum braking actuating force it is necessary to take moments about the
brake arm pivot point
The motion of the drum as shown result in an ACW friction moment and the normal reaction force of the drum also
results in an ACW moment as the two moments are the same self locking cannot occur. If the rotation is reversed
and the friction moment is CW then the resulting actuating force will be reduced and self-locking is possible.
|
Links to external brake block Design
|
|
Brakes