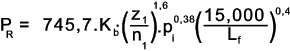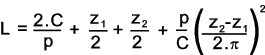Introduction
The roller chain is used to transmit motion between rotating shafts via sprockets mounted
on the shafts. Roller chains are generally manufactured from high specification
steels and are therefore capable of transmitting high torques within compact space envelopes.
Compared to belt drives the chain drives can transmit higher powers and can be used for
drives with larger shaft centre distance separations.
In European /ISO standards the chains are normally rated on a standard 15000 hours life. Service factors
on the drive and driven wheels are used to adjust the rating for non-standard conditions.
Chain Details
|
Typical Chain Arrangement
|
Relevant Standards
BS ISO 10823:1996 ..Guidance on the selection of roller chain drives.
BS 228:1994 ISO 606:1994..Specification for short-pitch transmission precision roller chains and chain wheels
Chain Description
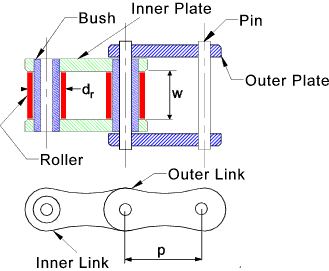
Roller /Transmission chains are identified using three measurements
- The pitch - centre distance between rollers (p)
- The width between the inner plates (w)
- The roller outside diameters (d r)
|
Chains manufactured to British/ISO standards can be supplied as single strand (SIMPLEX), double
strands (DUPLEX), or triple strands (TRIPLEX)..

Duplex Chain
|

|
The range of pitch sizes can vary between 4mm, (0.158 inch) to 114.3mm, (4.500 inch).
The European/ISO chain standards have large pin diameter compared to the US standards,
especially for the larger pitch sizes. This results in better wear
resistance due to the greater bearing area.
The ISO standard has a simple form of part numbering, for example:
1/2 inch pitch duplex chain would be 06B-3.
The first two digits are the pitch size in 1/16?s of an inch, therefore 06 = 6/16 or 3/8 inch.
The letter ?B? indicates European Standard.
The suffix 3 indicates the number of strands in the chain, in this case a triplex chain.
Chain Wheels /Sprockets
Chain wheels can be produced with a minimum of about 9 teeth but in practise the
minimum number of teeth is normally restricted to about 19 teeth. For special
applications requiring smoother drives a the smallest sprocket should not have less than
23 teeth.
The maximum number of teeth on the larger wheel should not exceed 150 and generally the number
of teeth is restricted to 114 providing a normal maximum ratio of about 6:1
The angle of contact of the chain and the smallest wheel should exceed 120o. This
provides practical limitation on the size of the larger wheel or results increased center distance
separation. Larger wheel diameters tend to result in reduced chain life.
It is good practice on low ratio chain drives to ensure that the number of teeth on
both wheel when added do not exceed 50. A 1:1 drive should therefore have a maximum of 25 teeth
on each wheel.
The large sprockets on high ratio drives are generally made of cast iron because the teeth
have reduced chain engagements over time with consequent reduced fatigue and wear.
For more arduous service conditions the larger sprockets may be made from cast steel or
steel plate. The smaller sprockets when highly loade are generally made from
steel type which allow the body to be heat treated for toughness while the teeth are hardened to resist wear e.g.
case hardened. Heat treatment is generally required when :
- The speed is above 0,7 time max speed when fully loaded
- The speed is above 0,5 time max speed when fully loaded, under medium impulsive load
- When the load is highly impulsive
|
Typical maximum speed are listed in the chain properties table below
For lower duties sprockets are generally machined from steel bar stock.
Idler sprockets
hen the drive and driven sprockets centres are fixed it may be desireable
to include idlers sprockets to take up the slack in the chain. Idler
sprockets should preferably be located against the slack side of the chain within
the chain envelope - diverting the chain outwards. Idler sprockets are
subject to continuous impact from the chain and are subject to wear if only small
sprockets are used and if the chain speed is high.
Chain System Design
A large number of roller chains are designed to provide a power transmission between two
sprockets with minimum/no regular lubrication and under conditions of high levels of contamination.
My bicycle chain drive has worked successfully for over 25 years ( including one replacement of the wheel sprocket
and one replacement of the chain). The bicycle is used at least three journeys per week for an average
journey time of about 20 minutes.
Motor cycle chain drives work in similar operating conditions...
Industrial chain drives are generally designed to operate in enclosed cases with installed lubrication systems.
Chains rarely fail because they do not have sufficient tensile strength. They most often
fail in wear or fatigue. In practice sprocket teeth wear allowing the chains to jump
the teeth. Manufacturers specify the chains based on the following parameters
- 15000 hours life
- Single strand
- ISO proportions
- Service factor (Application factor) =1
- Recommended lubrication
- Maximum elongation 3%
- Horizontal Shafts
- Two 19 tooth sprockets
- Sprocket centres = 40 pitches
|
Chain systems are designed with correction coefficients to compensate from the difference
from these design conditions
It is important when designing chain drives to ensure good alignment of the sprocket
shafts. It is also important to minimise chain slackness and if the centres
can not be adjusted then it may be necessary to use idler sprockets.
Chain Lubrication
Chain drive lubrication provides similar benefits to bearing journal lubrication. The benefits include
reduced friction, cooling, impact resistance at higher chain speeds. The chain supplier generally
provides recommendations for the lubrication requirements for each chain drive. If suitable lubrication
is not provided the then capacity of the chain drive is reduced.
There are four basic types of chain lubrication..
- Manual /Drip lubrication..In manual lubrication oil is generously applied to the chain
drive about every 8 operating hours. In drip lubrication oil is continuously dripped
on the chain centre line.
- Bath/Disc lubrication..In bath lubrication the lower strand of the chain runs through
a sump containing oil. The oil level should be above the lowest pitch line of the chain when it is operating normally.
Excessive immersion can result in turbulence of the oil bath. Disc lubrication is based
on a disc attached to one sprocket which is immersed in an oil bath. As the disc rotates
it picks up oil and deposit it onto the chain. A trough is often used to direct the oil
oil to the optimum point on the chain. A peripheral disc speed of between 3 and 40 m/s
- Oil stream lubrication...This is normally a continuous stream of filtered oil circulated
by a pump. The oil should be spread evenly across the width of the slack side chain
- Oil Mist lubrication...This is used for high speed chain drive and is based on the chain
case being filled with a oil mist.
|
There is continuous development in chain drives and self-lubricated chains are available
which do not require continuous lubrication and have similar performance to lubricated chain
drives.
Plastic chains are also available which do not require lubrication. Plastic
chain drives obviously have much reduced operating characteristics compared to steel chains.
Non-lubricated chains are essential for applications requiring controlled environments e.g.Paper,
packaging, electronics, white and brown goods manufacture.
Nomenclature
|
B a = Chain Bearing Area (mm2)
B s = Chain Bearing stress (MPa)
C = Centre Distance (m)
D1 = Drive sprocket Pitch Diameter (m)
D2 = Driven sprocket Pitch Diameter (m)
d r = Chain Roller Outside diameter (m)
f a = application factor
Ft = Torque developed tensile force in chain (N)
Fc = Centrifugal tensile force in chain (N)
f t = tooth factor
Kx (x = 1 to 8) = Correction Factors
L = Length of chain in pitches
T 1= torque on driver pulley (Nm)
T 2= torque on driven pulley (Nm)
Sd = Dynamic Factor of Safety
|
Ss = Static Factor of Safety
P 1 = Driver power Transferred (kW)
P 2 = Driven power Transferred (kW)= ηP1
m = Mass of chain / m (kg/m)
n 1= Driver sprocket rotational speed (rpm = m-1)
n 2= Driven sprocket rotational speed (rpm = m-1)
p = Pitch of chain (m)
v = Chain velocity (m/s>
w = Chain width between inner plates
η = Efficiency (normally about 98%)
z 1= Driver sprocket - Number of teeth
z 2= Driven sprocket - Number of teeth
|
Roller Chain Design Process
- Specify the Drive speed , Driven speed and the power to be transferred
- Identify the operating characteristics of the drive and driven shafts (smooth, rough, shock
- Select the approximate shaft centre distance
- Calculate the speed ratio using table of standard sprockets (minimum No of teeth normally 19
- Calculate the appropriate design factors
- Calculate the design power
- Select a chain which has a higher power capacity than the design power.
This will involve
some iteration
- Confirm that there is sufficient safety on the tensile strength of the chain and the
wear/fatigue strength of the bushing.
- C omplete the detail design of the sprocket shaft systems, guards, lubrication system etc
|
Torque on driver /driven pulley
If the input power = P1(kW) then the torque (Nm)=
T1 = P1 .9,549 / n
T2 = P1 .η 9,549 / n
Chain Velocity
The chain velocity (v)is calculated as follows
v = D1.π.n1 /60 (m/s)
= D2.π.n2 /60...(m/s)
Design Power For Chain
|
The design power is calculated as follows
Pd = P.K1.K2.K3.K4.K5.K6.K7.
K1. = Coefficient for teeth different to 19
K2. = Coefficient for Transmission Ratio
K3. = Application (Service) Factor
K4. = Centre Distance Coefficient
K5. = Lubrication Coefficient
K6. = Temperature Coefficient
K7. = Service Life Coefficient
Tooth Factor (K1)
Normally the drive is a reduction drive and the driver sprocket is the smallest. This is normally
selected as a 19 tooth wheel unless a high speed smoother drive is required then a 23
(or higher) tooth wheel is selected.
If a driver sprocket with z1 teeth
is select than a tooth factor ft is used.
Tooth factor ft = 19 / z1
Ratio Factor (K2)
This allows for the difference in ratio from the 3:1 ratio normally used in determining
the design power for chain drives...
| Ratio |
1:1 |
1:2 |
1:3 |
1,4 |
1,6 |
| K2 |
1,25 |
1,11 |
1,0 |
0,94 |
0,89 |
Table of Application Factor ..K3
| |
Driver Characteristics |
| Smooth Running, Electric Motors, IC engines with hydraulic couplings |
Some shock Loading..IC engines , Electric motors with frequent stops/starts |
Heavy shock Loading IC engines with less than six cylinders |
| Driven machine characteristics |
|
|
|
| Smooth running .Office Machines,Generators |
1 |
1,1 |
1,2 |
| Light duty ..Fans, pumps, compressors,printing machines, uniformly loaded conveyors, machine Tools |
1,2 |
1,3 |
1,4 |
| Moderate shock..concrete mixing , non-uniformly loaded conveyors, mixers. |
1,4 |
1,5 |
1,7 |
| Heavy shock loading.. Planars, presses, drilling rigs. |
1,6 |
1,7 |
1,9 |
Centre Distance Factor (K4)
This allows for chain designs with sprocket centre distances other than
optimum= C/p = 40.
| C/p |
20 |
40 |
60 |
80 |
=<160 |
K4
| 1,2 |
1 |
0,9 |
0,85 |
0,7 |
Lubrication Factor (K5)
This factor involves some judgement and the notes below are
provided for guidance.
- If the chain is correctly lubrication
and includes the recommended maintenance.
For self lubricated chain used correctly.
For very low duty chains
with reasonable lubrication:
A factor of 1 applies.
- If the chain is low - medium duty, provided with the recommended filtered lubrication but with average
maintenance.
A service factor of say 1,25 applies
- If the chain is medium to high duty, provided with lubrication
with average maintenance.
A service factor approx 2 - 3 applies.
- For a medium-high duty chain with no lubrication.
A service factor approx 5 will apply.
|
Temperature Factor (K6)
For all normal duties at normal ambient temperatures (0-80o C) the temperature
factor will be 1. For cases when a higher ambient temperature is normal a temperature
factor will be needed as table below....
| Deg.C |
0-80 |
80-150 |
150-250 |
| K6 |
1,0 |
1,1 |
1,2 |
Service Life (K7)
The power capacity of a chain is based on a 8 hour per day operating cycle and K7 = 1 .
For more arduous operating a different value of K7 is appropriate.
Operating time /day
hours |
0-8 |
8-16 |
16-24 |
| K7 |
1,0 |
1,1 |
1,2 |
|
Chain Power Capacities
The design power as evaluated by the above process should be less than the lower of the
chain capacity associated with the link or the bush as calculated below...Note: Manufacturers
and suppliers generally simplify this process by providing tables or charts to make this process more
convenient. A typical graph is shown below Chain Power graph....
Link- Power capacity
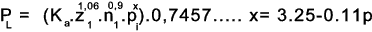
Bushing - Power capacity
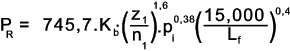
These capacities are modified by the strand factor Sf.
If there are two strands then the power capacity is increased by a S f = 1,7. If there are
three strands then the power is increased by a strand factor S f =2,5.
Pi = chain pitch in inches..
| Chain |
Ka |
Kb |
Chain |
Ka |
Kb |
Chain |
Ka |
Kb |
Chain |
Ka |
Kb |
Chain |
Ka |
Kb |
| 05B |
0.0046 |
17 |
10B |
0.0042 |
17 |
20B |
0.0046 |
17 |
32B |
0.0046 |
17 |
56B |
0.0038 |
7 |
| 06B |
0.0046 |
17 |
12B |
0.0044 |
17 |
24B |
0.0046 |
17 |
40B |
0.0032 |
17 |
64B |
0.0039 |
5 |
| 08B |
0.0048 |
17 |
16B |
0.0046 |
17 |
28B |
0.0046 |
17 |
48B |
0.0035 |
12 |
72B |
0.004 |
2 |
Tensile Load on Chain
The dynamic load on a chain includes for the tensile load for transmitting the power
and the centrifugal load resulting from the chain rotating on the sprocket.
For normal speed applications
only the direct load due to the tensile load is relevant.
Ft = P 1*1000 / v..(N)
Note this is derived in principle in the webpage for
flat belt drives.. Flat belts
The tension resulting for the centrifugal force =
Fc = Mm.v2..(N)
The resultant total tensile force taken by the chain =
Fr = Ft + Fc
The value Fr is divided into the breaking strength of the chain Fb
to obtain the static Factor of Safety of the Chain
Ss = Fr /F b
This value of Ss is divided by the Application factor K3 to arrive at the
dynamic Factor of Safety
Sd = Fr / (Fb * K3)
The graphs below show (very approximately) the range of recommended static and dynamic safety
factors.
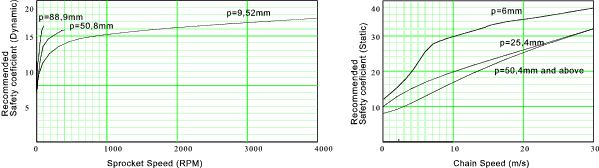
Chain Bearing Stress
The bearing stress is the resultant tensile stress / the bearing area Ba. Values for the
bearing area are provided in the chain properties table below...
B s= Tr / B a
The calculated bearing stress should be less than the acceptable bearing pressure
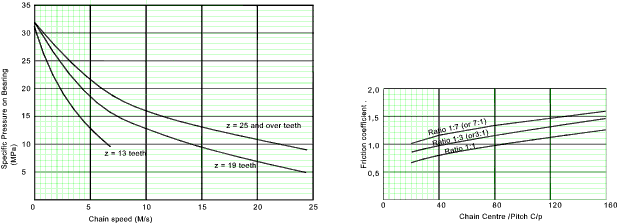
The acceptable bearing pressure = Specific Pressure .K9.K8.
K9 = 1 For ISO chains
K8 = The friction coefficient / K3
K3 = Service_application factor (K3) -see below
The specific pressure and the friction coefficents are obtained from the charts below:
Pitch Diameter
The pitch diameter of a chain sprocket can be obtained from the formula
D = P / sin (π / z)
Table below identifies the pitch diam for sprockets with chain pitch of 25,4mm .
for other chain pitches the diameter will be proportional e.g for 12,7mm chain pitch the
diameters will be half the tabled values.
Table of pitch diameters for 25,4mm pitch chain sprockets
| No Teeth |
Pitch Dia |
No Teeth |
Pitch Dia |
No Teeth |
Pitch Dia |
No Teeth |
Pitch Dia |
No Teeth |
Pitch Dia |
No Teeth |
Pitch Dia |
| |
mm |
|
mm |
|
mm |
|
mm |
|
mm |
|
mm |
| 10 |
82.20 |
30 |
243.00 |
50 |
404.52 |
70 |
566.15 |
90 |
727.80 |
110 |
889.48 |
| 11 |
90.16 |
31 |
251.07 |
51 |
412.60 |
71 |
574.23 |
91 |
735.89 |
111 |
897.56 |
| 12 |
98.14 |
32 |
259.14 |
52 |
420.68 |
72 |
582.31 |
92 |
743.97 |
112 |
905.65 |
| 13 |
106.14 |
33 |
267.21 |
53 |
428.76 |
73 |
590.39 |
93 |
752.05 |
113 |
913.73 |
| 14 |
114.15 |
34 |
275.28 |
54 |
436.84 |
74 |
598.48 |
94 |
760.14 |
114 |
921.81 |
| 15 |
122.17 |
35 |
283.36 |
55 |
444.92 |
75 |
606.56 |
95 |
768.22 |
115 |
929.90 |
| 16 |
130.20 |
36 |
291.43 |
56 |
453.00 |
76 |
614.64 |
96 |
776.31 |
116 |
937.98 |
| 17 |
138.23 |
37 |
299.51 |
57 |
461.08 |
77 |
622.72 |
97 |
784.39 |
117 |
946.07 |
| 18 |
146.27 |
38 |
307.58 |
58 |
469.16 |
78 |
630.81 |
98 |
792.47 |
118 |
954.15 |
| 19 |
154.32 |
39 |
315.66 |
59 |
477.24 |
79 |
638.89 |
99 |
800.56 |
119 |
962.24 |
| 20 |
162.37 |
40 |
323.74 |
60 |
485.33 |
80 |
646.97 |
100 |
808.64 |
120 |
970.32 |
| 21 |
170.42 |
41 |
331.81 |
61 |
493.41 |
81 |
655.05 |
101 |
816.72 |
121 |
978.40 |
| 22 |
178.48 |
42 |
339.89 |
62 |
501.49 |
82 |
663.14 |
102 |
824.81 |
122 |
986.49 |
| 23 |
186.54 |
43 |
347.97 |
63 |
509.57 |
83 |
671.22 |
103 |
832.89 |
123 |
994.57 |
| 24 |
194.60 |
44 |
356.05 |
64 |
517.65 |
84 |
679.30 |
104 |
840.98 |
124 |
1002.66 |
| 25 |
202.66 |
45 |
364.12 |
65 |
525.73 |
85 |
687.39 |
105 |
849.06 |
125 |
1010.74 |
| 26 |
210.72 |
46 |
372.20 |
66 |
533.82 |
86 |
695.47 |
106 |
857.14 |
126 |
1018.82 |
| 27 |
218.79 |
47 |
380.28 |
67 |
541.90 |
87 |
703.55 |
107 |
865.23 |
127 |
1026.91 |
| 28 |
226.86 |
48 |
388.36 |
68 |
549.98 |
88 |
711.64 |
108 |
873.31 |
128 |
1034.99 |
| 29 |
234.93 |
49 |
396.44 |
69 |
558.06 |
89 |
719.72 |
109 |
881.39 |
129 |
1043.08 |
Chain Centre Distance
There are practical limitations for the minimum distance between the chain sprocket
centres to prevent interference of the sprocket teeth. To provide a
reasonable chain operating life is necessary to
ensure good spacing and a minimum wrap of 120o. The drive layout
will determine the actual centre distance. A recommended value is about 40 time
the chain pitch.
When the chain centre distance can be adjusted to suit the chain length then the length (L)
of the chain in (pitches) can be used to determine the centre distance between sprockets (C)
using the following formula
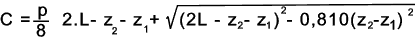
Chain Length
The length of the driving chain is normally required in numbers of double pitches because
a complete link includes the inner and the outer link which covers two pitches.
The Chain length (L) in pitches (p) is given (to sufficient practical accuracy ) by the formula
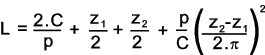
Chain Properties
Values are from BS 228 , ISO 606
The normal maximum velocity relates to sprockets with 17-25 teeth.
| Pitch |
Normal
max vel.
| Chain Identity |
Breaking
Force
(F b) |
Mass/m
(m) |
Chain Brg
Area
(Ba) |
Chain Identity |
Breaking
Force
(F b) |
Mass/m
(m) |
Chain Brg
Area
(Ba) |
Chain Identity |
Breaking
Force
(F b) |
Mass/m
(m) |
Chain Brg
Area
(Ba) |
| (RPM) |
(N) |
kg/m |
mm2 |
|
(N) |
kg/m |
mm2 |
|
(N) |
kg/m |
mm2 |
| 8,00 |
5000 |
05B - 1 |
5000 |
0.2 |
11 |
05B - 2 |
7800 |
0.4 |
22 |
05B - 3 |
11100 |
0.5 |
33 |
| 9.525 |
4200 |
06B - 1 |
9000 |
0.4 |
28 |
06B - 2 |
16900 |
0.8 |
56 |
06B - 3 |
24900 |
1.2 |
84 |
| 12.7 |
3750 |
08B - 1 |
18000 |
0.7 |
50 |
08B - 2 |
32000 |
1.3 |
101 |
08B - 3 |
47500 |
2 |
151 |
| 15.875 |
2750 |
10B - 1 |
22400 |
0.9 |
67 |
10B - 2 |
44500 |
1.8 |
134 |
10B - 3 |
66700 |
2.8 |
202 |
| 19.05 |
2000 |
12B - 1 |
29000 |
1.2 |
89 |
12B - 2 |
57800 |
2.5 |
179 |
12B - 3 |
86700 |
3.8 |
268 |
| 25.4 |
1500 |
16B - 1 |
60000 |
2.6 |
210 |
16B - 2 |
110000 |
5.2 |
421 |
16B - 3 |
165000 |
7.7 |
631 |
| 31.75 |
1200 |
20B - 1 |
95000 |
3.8 |
296 |
20B - 2 |
170000 |
7.5 |
591 |
20B - 3 |
250000 |
11.2 |
887 |
| 38.1 |
900 |
24B - 1 |
160000 |
7 |
554 |
24B - 2 |
280000 |
13.9 |
1109 |
24B - 3 |
425000 |
20.7 |
1663 |
| 44.45 |
700 |
28B - 1 |
200000 |
9.1 |
739 |
28B - 2 |
360000 |
18 |
1479 |
28B - 3 |
530000 |
27 |
2218 |
| 50.8 |
550 |
32B - 1 |
250000 |
9.7 |
810 |
32B - 2 |
450000 |
19 |
1621 |
32B - 3 |
670000 |
28.3 |
2431 |
| 63.5 |
450 |
40B - 1 |
380000 |
16.8 |
1275 |
40B - 2 |
630000 |
33.5 |
2550 |
40B - 3 |
950000 |
43.3 |
3825 |
| 76.2 |
300 |
48B - 1 |
560000 |
25.9 |
2061 |
48B - 2 |
1000000 |
48.6 |
4123 |
48B - 3 |
1500000 |
72.5 |
6184 |
| 88.9 |
- |
56B - 1 |
850000 |
35 |
2791 |
56B - 2 |
1600000 |
70 |
5582 |
56B - 3 |
2350000 |
105 |
8373 |
| 101.6 |
- |
64B - 1 |
1120000 |
60 |
3625 |
64B - 2 |
2000000 |
120 |
7250 |
64B - 3 |
3100000 |
180 |
10875 |
| 114.3 |
- |
72B - 1 |
1400000 |
80 |
4618 |
72B - 2 |
2500000 |
160 |
9234 |
72B - 3 |
4000000 |
240 |
13850 |
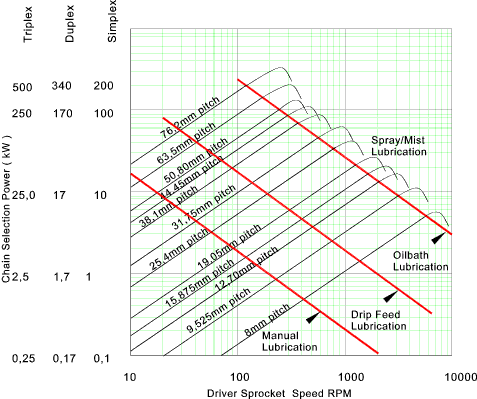
Typical graph of Chain Power Capacities
Note: I have hand sketched this based on a typical manufactures chart.. Please use it
with care and ,better still, get a the information from a chain supplier..
Chain suppliers each produce graphs similar to the one below to enable convenient
selection of a suitable chain for a specific duty. This is compared to the design
power which is the required power corrected by appropriate factors. The main factors
to be considered are the tooth factor and the service factor...
|