Nomenclature Dynamics Formulae
Linear Motion For constant velocity. Distance moved at constant velocity s = v . t For constant Acceleration from velocity v_o start. v = v_o + a . t Simple Harmonic Motion Simple Harmonic Motion is characterised by the relationship that the rate of
acceleration of a body towards a central position is directly related to the distance
of the body from the central position. f ''(x) = - ω2 . x The solution for the displacement from and the velocity towards the central position is below; x = a . cos ( ω. t + ε )
Newtons laws of Motion Newtons First Law;
Newtons Second law;
Newtons Third law
Momentum Momentum = m . v Force F = m . a Mass Moment of Inertia The mass moment of inertia of a body about an axis has been defined as the sum of the products of mass-elements and the square of their distance from the axis Rotary Motion For a mass rotating about a centre. The force tending to accelarate the mass
towards the centre and restraining the mass to move around the centre is the centripetral force.
The reaction to this force tending the accelarate the mass away is the centrifugal force.
(If the string breaks the mass would fly away under the effect of the centrifugal force. 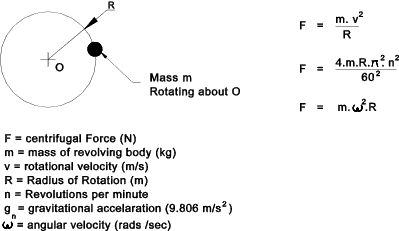 Acceleration Torque Angular acceleration α = (ω2 - ω1) / t Acceleration Torque T = I . α |
|
|
Formulae_Index
Nomenclature