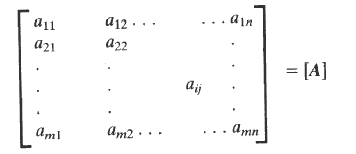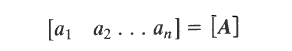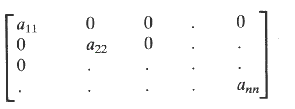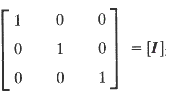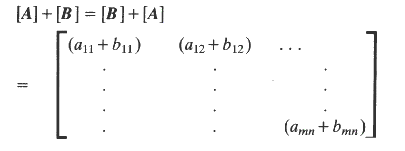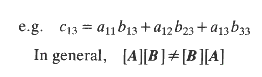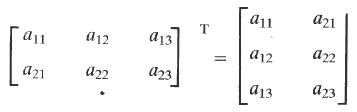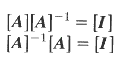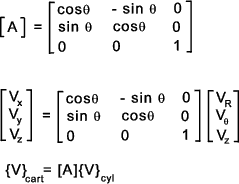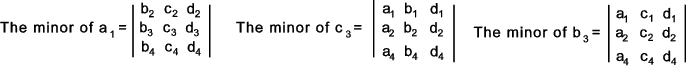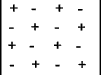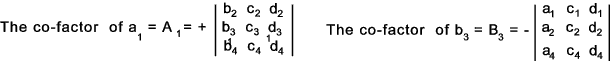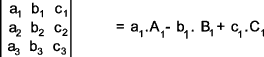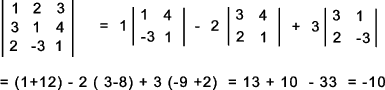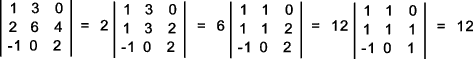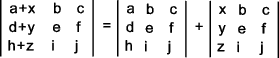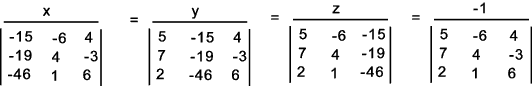Matrices and Determinants
|
Matrices Matrix calculus is a mathematical tool used in connection with linear equations , linear transformations, systems of differential
equations etc. Matrices are important in physics, engineering, statistics etc. y 1= a 11 x1 + a 12x 2 These equations can be expressed using Matrices as follows
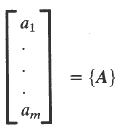
1) A matrix is an array of numbers . A matrix with m rows and n columns is order m x n and is shown as follows.. 2)A row matrix has one row of numbers as shown below:- 3) A column matrix has one column of numbers as shown below:- 4) A square matrix is one with an equal number of rows and columns i.e m = n 5) A diagonal matrix is a square matrix with all numbers zero apart from diagonal numbers as shown below:- 6) A unit matrix is a square matrix with all diagonal numbers = 1:-. The other elements being 0.. 7) A Symmetric matrix is one with a ij = a ji 8)A null matrix has all elements = 0 9)The addition of matrices are completed as follows:-
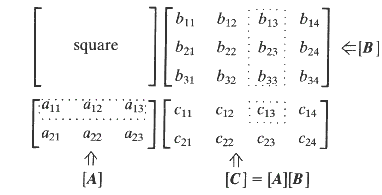
10) The multiplication of matrices are completed as follows:-
11) A Matrix is transposed so that each row element becomes a column element and vice-versa:-
12 )The inverse of a matrix is defined as follows:-
The inverse can be defined only a for square matrix.. There are cases where even a square matrix cannot
be so defined.
Determinants Determinants are Arrays which are very useful in the analysis and solution
of systems of linear algebraic equations. Generally the solutions are unmanageable
when written at length. Using determinants the equations become relatively simple expressions.
As and example consider the equations a1x + b1y + c1 =0 The solution is obtained in the form x / (b1.c2 - b2.c1 ) = y / (c1.a2 - c2.a1 ) = 1 / (a1.b2 - a2.b1 ) The denominators of this solution can be expressed simply in the form of determinants e.g.
The order of the determinant equations refers to the number of rows/colums e.g.
If the row and column of any element is deleted then a reduced order determinant remains which is called the minor determinant of the element in question..e.g. considering the fouth order deteterminant above..
Associated with each element is a sign (+ or -) this is established by counting the number of row and column steps to get from the first element and if the steps are 0 or even the sign is (+ ) and if the steps are odd the sign is ( - ). e.g.
The co-factor of and element is the minor of the element x the relevant sign. e.g.
The expansion of a determinant is completed by adding the product all of elements with their co-factors for any row or column. eg
An example of the expansion of a determinant is provided below..
The expansion of the determinant is simplified by using the row or column with zero elements if any as the
relevant element-co-factor is zero.. The value of a determinant is not altered if its rows are written as columns , in the same order..
If any two rows or any two columns are interchanged the result is a change in sign of the determinant... A determinant with two rows or columns equal has zero value.. If all the elements of one row (or one column) is multiplied by the same factor (say k) , the value of
the determinant is k x the value of the given determinant.
If all of the elements of a row or a column is zero then the value of the determinant is zero. If the elements of a row or column are expressed as a binomial the determinant can be written as the sum
An example of solving 3 linear equations can be expressed as
a1x + b1y+ c1y + d1 = 0 Using determinants this is solved by the following relationship<
Solve the equation.. 5x - 6y + 4z = 15 This equation is rewritten as 5x - 6y + 4z - 15 = 0 Expressing this in determinant form
On evaluating the denominators. ( x /-1257 ) = ( y /-1676 ) = ( z / -2514 ) = ( -1 /419 ) Dividing each denominator by 419 results in ( x /--3 ) = ( y /-4 ) = ( z / -6 ) = -1 This results inx = 3: y =4: z =6 |
Links to Matrices
|
|
Maths Index