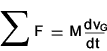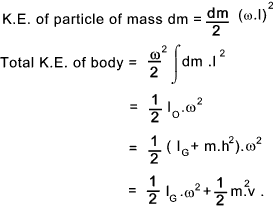The contents of this page are listed below

It is assumed that all motions are within the plane and rotations are around axes perpendicular to the plane. Infinitesimal counterclockwise rotations are positive and are therefore represented by vectors perpendicular to the plane as indicated by the right hand rule- If the plane is the x-y plane then angular velocities are in the positive z direction. It should be noted that large rotations and angular velocities do not follow vector rules..

A free body diagram is an extremely useful tool for assessing the interaction of forces on bodies       This is essentially a sketch of a body which is in equilibrium and is entirely separate from the surroundings.  The only rule for drawing free-body diagrams is to depict all the forces which exist for that object in the given situation.

Newtons First Law;
Every body continues in a state of rest or of uniform rectilinear motion unless acted upon by a force.

Newtons Second law;
The time rate of change of linear momentum of a body is proportional to the unbalanced force acting on the body and occurs in the direction in which the force acts.

Newtons Third law
To each action (or force) there is an equal and opposite reaction. The mutual force of the two bodies acting upon each other are equal in magnitude, opposite in direction and are collinear.

The momentum is defined simply as the product of mass and velocity..The first law states that if a body changes its velocity then a force must have been applied. The second law establishes a relationship between the magnitude of the force and the change in momentum..

Force    =   k. d(momentum)/dt    =   k.d(mv)/dt    =   k.m dv/dt    =   k.m. a

In the metric ISO system the unit of force of 1 Newton (N) on a mass of 1 kg results in a linear acceleration of 1 m/s ² therefore k = 1.

Newtons third law states that if two bodies collide the total momentum after impact must equal the total momentum after impact.   For two colliding masses (m₁ & m₂ ) with initial velocities ( u ₁ & u ₂ ) and final velocities ( v ₁ & v ₂ ) ..

m ₁. u ₁ + m ₂. u ₂ = m ₁. v ₁ + m ₂. v ₂ ... therefore m ₁ . ( v ₁ - u ₁ ) = m ₂( v ₂ - u ₂ )

1) Force = constant value.. F = C= constant = mass x acceleration..

m. dv/dt = C
dv = C/m dt

Falling masses under the effect of gravity provides an example of this condition
The motion of the particle can be determined by integration provided the initial conditions are known..

2) Force is a function of time F = F(t)

m.dv/dt = F(t)
dv = 1/m F(t)dt

Using F(t) the equation for the velocity can be determined by integration, and again the displacement can be found from ds = vdt.

3) Force is a function of velocity.

m. dv/dt = F(v)
dt = m.dv / F(v)

Example: The resistance to motion of drag or viscous damping when the force = C x velocity where c = the damping coefficient..

4) Force is a function of Displacement.

m. dv/dt = F(s)
because a.ds = v.dv then m. v.dv = F(s).ds

Example : The force developed by spring = k x s where k is the stiffness of the spring.

A mass rotating in a circle is accelerating towards the centre of the circle at a rate of acceleration of v² /r. The force pulling the body into the centre of the circle is the centripetal force. (if the mass is spinning on a string the centripetal force is the tension in the string). The reaction force at the centre of the circle is the centrifugal force.   There is no force pulling outwards on the circling body there is only a force pulling in

Considerations of rigid objects are simplified if ...
M = The mass of the object which is concentrated at a point which is at the mathematical centre of mass
r_G = The position of the centre of Mass relative to the co-ordinate origin.

The vector sum of the external forces acting on a set of particles (rigid body) equals the total mass times the accelaration of the centre of mass, irrespective of the motion of the separate particles.

The moment of Inertia of a particle of mass dm at a radius r from a axis through the centre of gravity G is dm.r ². The moment of inertia of the whole body about the axis through G =

This is generally written as

Where k is termed the radius of gyration.


The angular motion of a mass of inertia I_G is related to an applied torque as follows

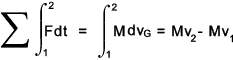
T= applied torque and α = angular acceleration..

The relationship between force and the motion of a mass as shown above can be written as..

This can be integrated to..

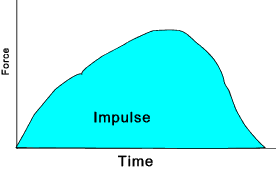
Impulse = change in momentum

The impulse is effectively the area under a plot of the force-time relationship

The angular impulse of a constant torque T acting over a time t is the product of Tt.   (If the torque varies the angular impulse is the integral or the area under plot of Torque-time relationship. )

The result of this torque on a mass of inertia I_G

That is the impulse of torque = change in angular momentum..

The transfer of energy expressed as the product of a force and the distance through which its point of application moves in the direction of the force. ... It should be noted that work only results if the point of application of the force moves.   There is no work done if a weight is supported without movement.

If a force is acting on a particle as it move from A to B . The work done as the particle moves a small distance dr = F. dr . The work done is the product of the Force vector and the displacement vector.   Only the force component in line with the displacement component contributes to the work done. Work is a scalar quantity and is measured in N.m (ISO units)

The work performed by a force F (N) when the point of application moves S (m) with angle q between the force and the direction of motion .

Work (U) = F.cosθ .S

The work performed by a couple M turning an object through an angle θ is

Work (U) = Mθ

Work is a scalar quantity..

The work done by a force extending/compressing a spring (in the x direction) is calculated as follows:

If the work done by a force is independent of the path the force is called a Conservative force.  Examples of conservative forces include spring forces and gravitational forces.   Conservative forces are generally recoverable ; that is if work is done in lifting an object against gravity through a vertical height h , the work is is recovered by lowering the weight back to the original level.

When force is required to move an object to overcome friction the energy dissipated cannot be conveniently recovered as work   The work done against friction is not available as kinetic or potential energy.  The work done by a non-conservative force is dependent on the path taken by the point of application of the force..

At its simplest level energy is defined as the ability to do work.  Energy takes many forms including kinetic energy, potential energy, thermal energy, chemical energy, electrical energy, and atomic energy.

The field of mechanics includes kinetic energy which is energy possessed by a body due to its motion and potential energy which is energy possessed by a body because of its position in a field force (gravity /elastic force).


The kinetic energy increase of a mass subject to a force is derived as follows..

The term   m.v ² / 2   is called the kinetic energy of the mass and hence the derivation above results in

Work Done by a force on a mass = change in kinetic energy.

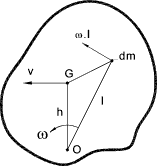
A body is rotating about and axis through O.

If the centre of gravity of a body is moving with a velocity v and is rotating with and angular velocity of w about the centre of gravity.

The total K.E. = K.E. of translation + K.E. of rotation

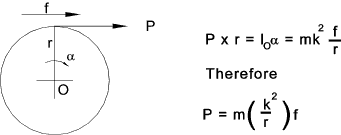
When considering motions of machines with comprising masses in linear motion and masses with and angular motions it is often required to find the equivalent mass of a rotating body.   This occurs often with vehicle dynamics. In considering a body of mass ( m ) rotating about an axis through O with a tangential force at radius ( r ) producing a linear accelaration at this point of ( f ) with and a resulting angular accelaration of (α ).

The quantity   m.( k / r ) ²   is the equivalent mass of the body referred to the line of action of P.


This relationship can be used to convert a system with rotating masses and linear mass e.g. a vehicle into a system comprising equivalent linear motions only.

In general terms potential energy identifies some form of stored energy which can be converted into some other form of energy. Potential energy take many forms including mechanical, chemical, electrical nuclear etc.   These notes only consider mechanical potential energy which is energy stored by a body because of its position with respect to a datum is a conservative force field.   The two most common forms of potential energy in mechanical engineering are gravitational potential energy and elastic strain energy..

The force on an object in the earths gravitational field is directly related to the mass of the earth and the object and is inversely related to the square of the distance between the centre of the earth and the object.  For normal mechanical considerations close to the earths surface the force is simply express as follows

F_G = m.g

where g = the gravitional constant (acceleration due to the attraction of the earth) ..This is generally approximated to 9.81 m/s² but can vary at due to variations resulting due the fact that the earth is not a perfect even sphere and due to the effect of other celestial bodies.

At it simplest level the Potential energy change due to gravity for a mass m moving from h₁ to h₂ =

PE = g.m (h₂ -h₂ )

An example of the elastic strain potential energy is the extension or compression of a spring as noted above..

The principle of conservation of energy in it simplest form states
[ The total amount of energy in the universe is constant: energy cannot be created or destroyed although in may be converted into various forms..]
.
In the field of mechanics the general energy principle is simplified to consider only the energy related to motion and position..
[If a system of bodies in motion is only under the action of conservative system of forces , the sum of the kinetic and potential energies of the bodies is constant.]

In its more general form the general energy principle may be stated as
[The work done on a system is equal to the change in kinetic energy + potential energy + losses ]

Power is defined as the rate of doing work.

Power = P = dW/dt = F. dr /dt = F.v

Power is a scalar quantity with units N.m/s