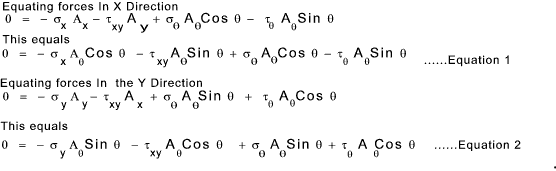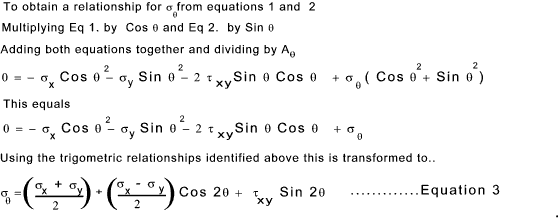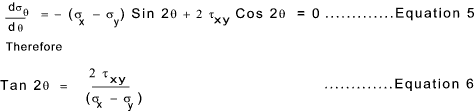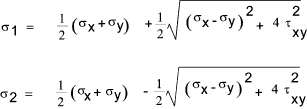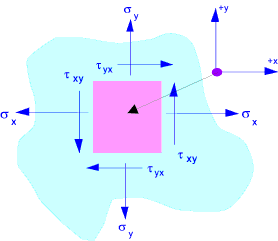
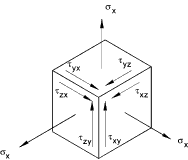
In considering plane stress i.e. stress in the x-y plane the z plane is assumed to be stress free   Three dimensional stress analysis is similar in principle but a bit more complicated.   The diagram below represents a small point in a solid which is under stress in the x and the y direction.  The point is in equilibrium so forces in the x direction are balanced as are forces in the y direction. Also clockwise (cw) moments balance counter clockwise moments(ccw).   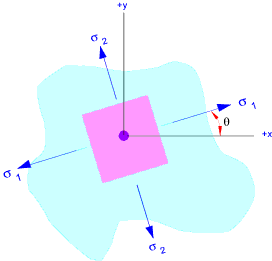Therefore τ _xy = τ _yx The figure below represents a two dimensional loading regime with a tensile stress (+ ve) σ_x in the x direction and a tensile stress (+ve) σ_yin the y direction.   A counterclockwise (-ve)shear stress τ _xy on the x surface and a balancing clockwise shear stress (+ve)shear stress τ _xy on the y surface..

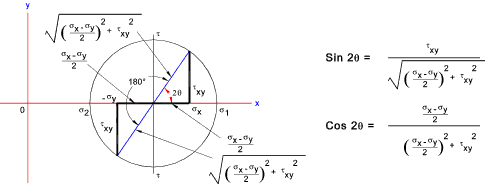
If the x-y axes is rotated the various stress will also change. There is an angle θ at which normal stresses will be a maximum and minimum.   At this angle there will be zero shear stress.  These stresses are called the principal stresses.

The principles stresses are identified as σ₁, σ₂ and σ₃... ( σ₁ > σ₂ > σ₃ ).

If a two dimensional stress regime is under consideration it is important that the missing principal stress should be assumed to be zero.

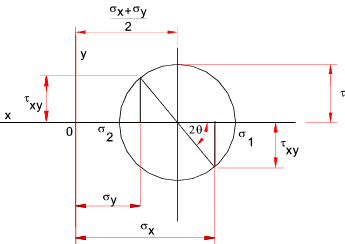
Mohr's Circle is a simple graphical method of showing stresses and strains within objects subject to loading enabling convenient visualisation and evaluation of developed stresses and strains at different axes to the generating loads. i.e. The graphical representation of the variation of the stress and strain components resulting from rotating coordinate axes.  Mohr's circle can be used for convenient representation of 3 dimensional stress strain distributions.

A typical Mohr's circle diagram is shown below:

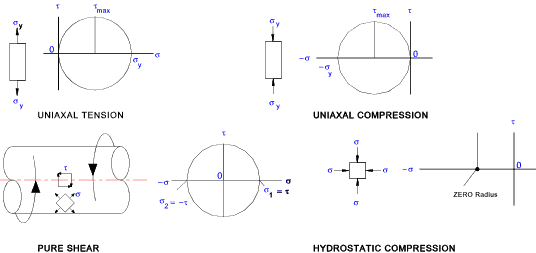
Mohr's circles representing different stress regimes are shown below:

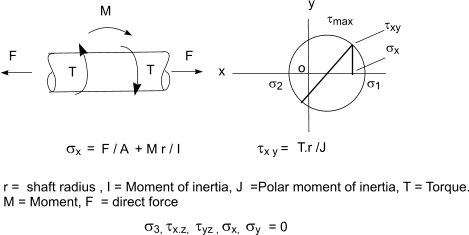
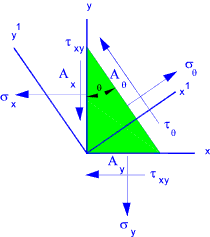
For a typical application of a shaft subject to direct stress, torque, and a bending moment the mohrs circle is as follows

When completing two dimensional assessments it should be recognised that solids are actually three dimensional and the stress distribution is actually as shown below..

There are always three principal stresses - (though one of the principal stress may be zero). Some typical three dimensional mohr's circle diagrams are shown below..

The following Trigometric relationships apply.

Cos θ² =(1 + Cos (2θ) ) /2

Sin θ² =(1 - Cos (2θ) ) /2

Sin θ Cos θ = Sin (2θ) /2

Analysing the resulting stresses when rotating the axes

Consider a rotated small element

A _x = A _θ. Cos (θ )

A _y = A _θ. Sin (θ )

By differentiating σ_θ with respect to θ and equating to zero the conditions for the maximum and minimum stress can be determined

The the two solutions satisfying this condition are illustrated in the figure below.

By comparing equations 4 and 5 above it is clear that at the angle resulting in the principal stresses (max and min) the shear stresses are 0...
Substituting the values for Sin 2θ and Cos 2θ into equation 3 results in formulas for the principles stresses σ₁ and σ₂..