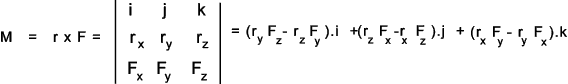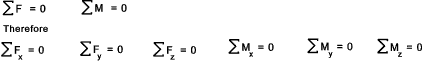Statics deals equilibrium of stationary bodies and bodies moving at constant velocity.
The notes on this page include use of vectors. The necessary background information is provided on page Vectors

A force identified as a localised vector it requires point of application, magnitude and direction.

The contents of this page are listed below

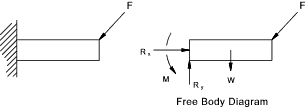
A free body diagram is an extremely useful tool for assessing the interaction of forces on bodies    This is essentially a sketch of a body which is in equilibrium and is entirely separate from the surroundings.  The only rule for drawing free-body diagrams is to depict all the forces which exist for that object in the given situation.   Below is shown a typical 2- dimensional free body diagram of a cantilever beam

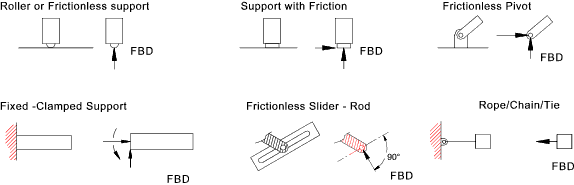
The free body diagram includes external forces applied to the body and external reaction forces resulting from the method of supporting the body.    Some reactions are shown in the 2-dimensional figure below.

A force can be represented by a localised vector defined by magnitude, direction and point of application .   A number of forces applied to any point can be replaced by a single resultant force using the principles of vector addition as shown on the vector page of this website.. From Newtons's first law it is is known that a particle will remain at rest if all the resultant force on the particle = zero . This called the equilibrium condition.. Using cartesian co-ordinate system this may be states as follow;

or

This is simplified by by considering only the scalar identities..

Since there are three equations of equilibrium for the three dimensional case, there can be at the most three unknowns which can be determined from these equations..

A moment applied to a body creates a tendency for the body to rotate.. The moment of a force about a point equals the product of a distance (say r ) = the lever arm and the force (F) acting perpendicular to the lever arm..

The moment of a force is defined in vector form using determinant algebra (in 2 dimensional and 3 dimensional cases) as

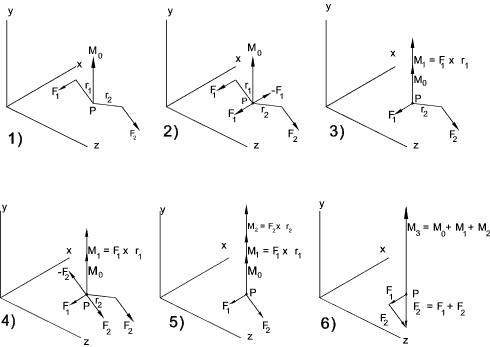
( refer to notes on Matrices/Determinants Matrices /Determinants
If a number of concurrent forces are applied to a point P and r is the position vector from 0 to P. the moment caused by these forces =

M_o = r x (F₁ + F₂ + F₃...) = r x F₁ + r x F₂ + r x F₃...

That is the moment due to several concurrent forces is equal to the sum of the moments of the indivual forces.

If two forces are equal in magnitude (F), parallel in line of action on opposite in direction they result in a couple. The magnitude of the moment of the couple is the distance between the force (e) multiplied by one force. The direction of the couple is identified by the right hand rule....

Couple = e x F

It can be proved that the moment of the couple is the same magnitude at any location...

If a number of forces are applied to a body resulting in a number of moments the moments can be combined algebraically to a resultant moment with a force.. An example below shows how two offset forces and a single moment can be combined to a resultant force and moment..

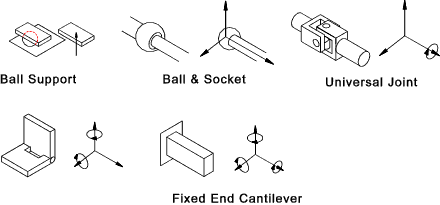
A particle is in equilibrium if the resultant force acting upon it is zero... A rigid body is in equilibrium if the resultant force is zero and if the resultant moment = 0...

There are therefore at the most 6 independent equations of equilibrium. The six equations are obtained from the free body diagram showing all of the applied forces and moments and also all of the resulting reaction forces and moments. From these six equations it is possible to solve for six unknowns..  If there are more than six unknowns then the system is statically indeterminate...

For the special case of 2 dimensional equilibrium which is most often applied for beams and simple structures the equilbrium equation as below is used...

A number of support systems with the resulting reactions are shown below...

Any assemblage of materials whose function is that of supporting loads is a structure.. The term may be applied to a bridge, and aeroplane wing a building or a dam.   The component parts of a loaded structure are in a state of stress and the laws which govern the distribution of the stress are used to calculate the design a material to enable the structure to safely support the loads.

Structures are classified into two general groups : framed structures and mass structures. The former is based on a number of separate bars or plates pinned, rivetted or welded together as a lattice.   These depend upon the geometric properties of the arrangement to withstand the load.   Mass structures depend upon the mass of material in the structure to withstand the resistance to the load e.g a masonary damn.   The notes following relate only to framed structures.

The notes that follow relate to frameworks or trusses.   These are arrangements of bars connected at pin joints which do not transmit moments.  The connecting bars are only allowed to transmit tensile forces (Ties) or compressive forces (struts).  It is assumed that the struts and ties experience virtually zero deformation.

For a plane frame (2- dimensional) the number of bars (N) required with J joints.

N = 2.J -3

For a space frame (3- dimensional) the number of bars (N) required with J joints.

N = 3.J - 6

Note:
Although the notes relate to frames with pinned joints it is clear that in practice most frame joints are not pinned .     The principles can be used with reasonable accuracy for the majority of frames when the ratio of the length of the member to its depth (L/d) is greater than 10. For frames with relatively rigid joints and short members the analysis is statically indeterminate and outside of the scope of this website.

There are three methods of assessing frameworks

The steps in this procedure are listed as follows.

Note: this method is convenient for simple frames but is very complicated for larger frames and cannot be used for space frames (3 -dimensions).

The steps in this procedure are listed as follows.

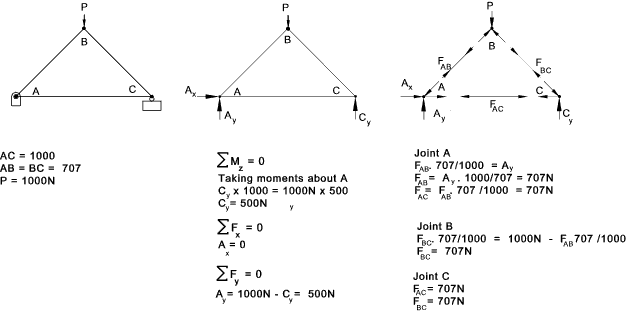
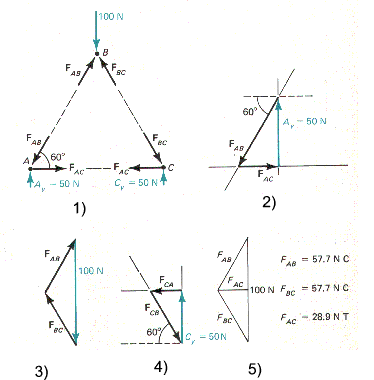
An simple example is provided below..

The steps 1,2 & 3 above have been ommited as they are relatively obvious
1) below includes a free body diagram for the each of the joints
2) below is a polygon of forces for joint A. The forces in the bar directions are drawn to scale.
3) below is a polygon of forces for joint B. the forces in the bar directions are drawn to scale.
4) below is a polygon of forces for joint C. The forces in the bar directions are drawn to scale.
5) below is a combined force diagram (Maxwell diagram ) for the truss..

Note: This method can be used to determine the forces in selected bars more rapidly then with the method of joints in some cases..

The steps in this procedure are listed as follows.

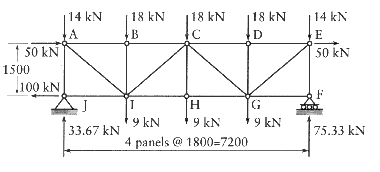
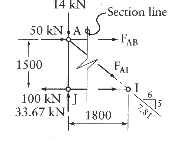
An example illustrating the method of sections is shown below; The object is to determine the forces in members AB and JI

A section line is drawn through the members under consideration and a free body diagram is drawn for the part of the structure to the left of the section line...

The unknown forces are shown in tension.
Taking moments about joint A eliminates Forces F_AI and F_AB leaving only the force F_JI.
Sum Moments about A to zero.
0 = 100.(1,5) - F_JI.(1.5) therefore F_JI = +100kN (tension)

Taking moments about joint I outside of the free body, eliminates F_AI and F_JI leaving only F_AB
Sum Moments about I to zero.
0 = 50.(1,5) - 14.(1,8) +33,67.(1,8) + F_AB therefore F_AB. (1,5) = -73,60kN (tension)

Summing moments vertically to zero eliminates both F_JI and Force F_AB leaving only F_AI
0 = 33,67 -14 - F_AI (5 / 7.81) therefore F_AI = +30,72 (tension)

F_JA = -33.67kN (compression) by expansion

Forces are represented as vectors with magnitude direction and point of application.. In reality most forces are applied overspecified areas.   If the area over which the force is applied in relatively large the force is considered to be a distributed force.  In these cases the method of approach is to reduce these distributed forces to single point which is the resultant of the distributed forces.   An example of this is the weight of a component which is considered to act at the centre of gravity of the component.