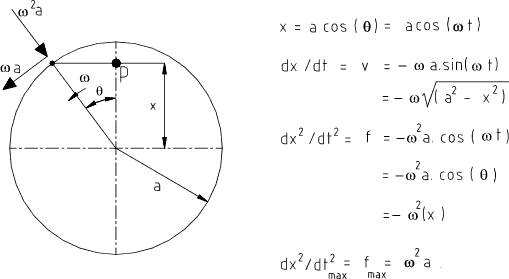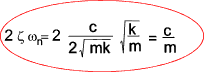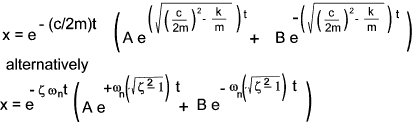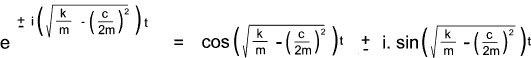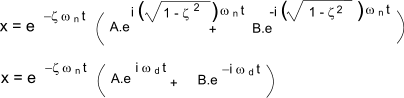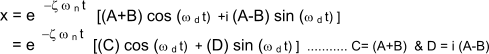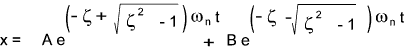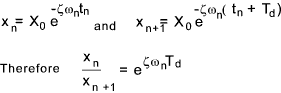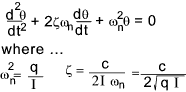Symbols
x = distance in x direction (m)
dx/dt = velocity in x direction (m/s)
d 2x/dt2 = acceleration in x direction (m/s2)
v = dx/dt = velocity (m/s)
f = d 2x/dt2 = acceleration (m/s2)
θ = angular rotation (radians)
dθ /dt = angular velocity (radians /s)
d 2θ /dt2 = angular acceleration (radians /s 2)
α= d 2θ /dt2 = angular acceleration (radians /s 2)
m = mass ( kg)
|
I = Moment of Inertia ( kg .m2)
k = spring stiffness (N/m)
c = coefficient of viscous damping (N s /m)
cc = critical damping coefficient.(N s /m)
ζ = Damping ratio = c / (2 m ωn ) = c / [ 2.m √ (k/m)]
π = pi
ω = angular velocity (radians /s)
ωn = Natural frequency (radians /s)
|
Simple Harmonic Motion
Generally free natural vibrations occur in elastic system when a body moves away from its
rest position. The internal forces tend to move the body back to its rest
position. The restoring forces are in proportion to the displacement.
The acceleration of the body which is directly related to the force on the body is
therefore always towards the rest position and is proportional to the displacement of the body from its rest position. The body moves with
simple harmonic motion...
Simple harmonic motion is most conveniently shown as the projection on the vertical (x) axis of a point rotating
in a circular motion (radius a) at a constant angular velocity ω.
The tangential velocity of the point = ω a.
The acceleration of
the rotating point toward the centre of the circle..= ω 2. a
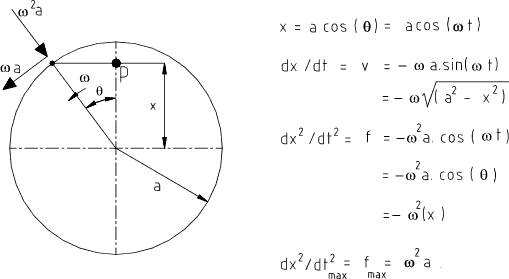
|
The time taken to complete on cycle = t p = 2. π / ω
The rotating speed (frequency of vibration) n = 1 / t p = ω / 2 . π
The acceleration dx 2 / dt 2 = f = ω 2 . x and therefore ω = Sqrt ( f /x )
Therefore n = Sqrt ( f / x ) . 1 / ( 2 π ) ..
|
Free Natural Vibrations
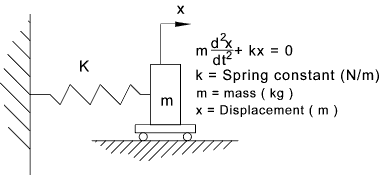
The extension of the spring results in a restoring force of F = k.x
The mass will accelerate at a rate directly proportional to the restoring force
The equation of motion of the above spring/mass system is therefore...m .dx2 / dt 2 = - k . x
This may be written as dx2 /dt 2 + ω n2 . x = 0 .......
( after making ωn 2 = k / m )
The "Natural circular frequency" = ωn ....... (units = rads/s)
Then "Natural frequency" n = ω n
( 2 π ) = Sqrt (k / m ) / ( 2 π ).....(units = cycles/s)
|
Damped Vibrations ..(Viscous Damping)
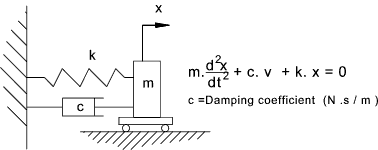
The resisting force of the damper is directly proportional to the velocity of the mass
The equation of motion of the above damper/spring/mass system is therefore
m.dx2 /dt 2 = - k.x - c.dx /dt
This equates to the general expression of the equation of motion of a ocillating system with damping
m.dx2 /dt 2 + c.dx /dt + k.x = 0
dividing throughout by m
dx2 /dt 2 + (c/m).dx /dt + (k/m ) .x = 0
Now by making ωn 2 = k / m
and by making ζ = c / (2 m ωn ) = c / [ 2.m √ (k/m)]
the following version of the equation results
dx2 /dt 2 + 2ζ ωn dx /dt + ωn2 x = 0
Note: ζ is called the damping ratio and is described a little better under heading critical damping ratio below.
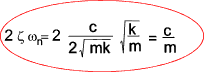
a bit complicated but simplifies the final analysis
The equation is solved by assuming a solution of the form x = e s.t (s = constant)
Substituting this relationship into the equation results in the formula
( s 2 + (c/m)s + (k/m) ) e st = 0 = ( s 2 + 2ζ ωns + ωn2) e st
Therefore ;
s 2 + s (c/m) + k/m = 0 = s 2 + 2ζ ωn s + ωn2
This equation has two roots
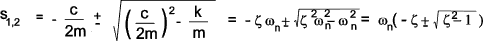
The solution of the equation in general forms
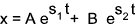
A and B are constants which can be evaluated from initial values of x and dx/dt..
The substitution of the roots into the general form results in the formula .
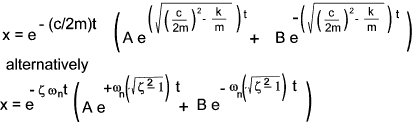
The term e - ( c / 2 m) t represents an exponentially decaying factor...The expression inside
the brackets can have three general results which significantly affect the solution.
1).. if (c /2 m) 2 = (k / m) .. (ζ 2 = 1 ) the factor inside the bracket is 0 and the solution is critically damped
2).. if (c /2 m) 2 < (k / m).. (ζ 2 < 1 ) the factor inside the bracket is negative : the solution is underdamped
3).. if (c /2 m) 2 > (k / m).. (ζ 2 > 1 ) the factor inside the bracket is positive and the solution is overdamped
4)..if (c /2 m) 2 = 0 ..(ζ 2 = 0 )The system is undamped
|
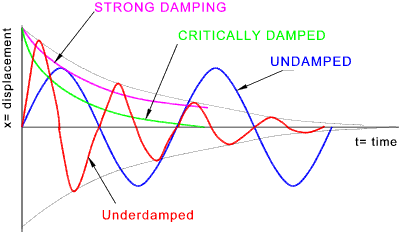
Critical damping ...( (c /2 m) 2 = (k / m) and ζ= 1 (see below) )
The damping value c which results in [ (c/2m) 2 - (k/m) = 0 ] is called
the critical damping coefficient cc
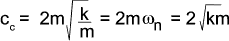
The damping can be expressed in terms of the damping ratio
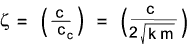
This results in the values..
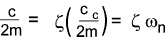
Underdamped Oscillations.. ( ζ <1 or (c /2 m) 2 < (k / m))
In the underdamped case the square root of a negative number is an imaginary number..resulting in roots of
This results in a oscillatory solution of the form..
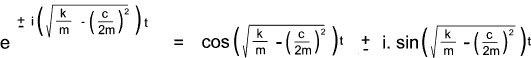
The frequency of damped oscillation (rads/s) is equivalent to
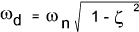
The equation of motion for the underdamped case ( ζ < 1 ) is rewritten as
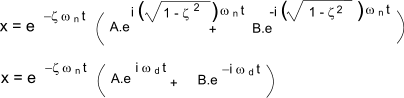
This equation can be transformed to
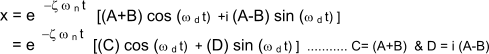
This equation can be further transform into an equation with one trigonometric term as follows
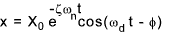

Overdamped Oscillations ....( ζ > 1 and (c /2 m) 2 > (k / m))
The equation of motion for the overdamped case ( ζ > 1 )is rewritten as
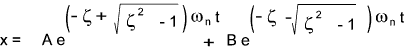
The equation of motion for the critally damped case ( ζ = 1 )is written as
Logarithmic Decrement....
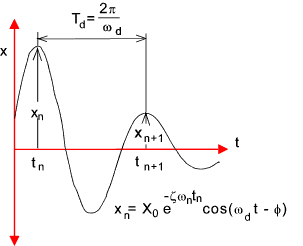
The rate at which the amplitude of vibrations decays over time provides a very useful method of
identifying the degree of damping. See the figure below for the plot of a typical underdamped vibration.
The equation for of motion for underdamped oscillations arrived at above can be used to establish the amplitude
of any of the cycles. i.e.
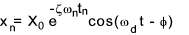
Considering the amplitudes of successive cycles when cos(ω dt - φ) = 1
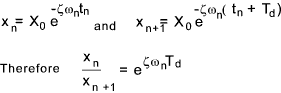
The logarithmic decrement δ is ln( xn / xn+1 ).. Normally n = 1 and n+1 is therefore 2.
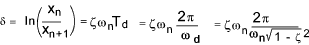
The damping ratio ζ can be expressed in terms of the logarithmic decrement δ
as follows
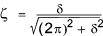
It is clearly possible to determine the damping ratio experimentally for a mechanical system be
initiating vibrations and measuring the amplitude of the vibrations.
Angular Vibrations
Consider a disc with a moment of Inertia I suspended
on a vertical bar with a torsional stiffness q with a viscous damper attached with a viscous damping coefficient c
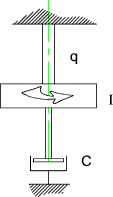
The equation of motion of this system is expressed by the equation ..
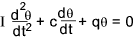
This equation can be expressed using the natural circular frequencey ωn and the
damping ratio ζ..
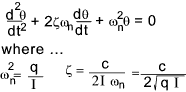
It is clear that this equation is the same as the equation of motion for linear motion as reviewed above and
can be analysed using the same principles
|