Introduction The information below relates to natrural frequency of traverse vibration. The units for the various
parameters must be consistent. i.e for metric calculations length is m, force = N, mass = kg. etc. Nomenclature The units below relate to application of the equations using SI metric values
It can be shown that the critical whirling speed for a shaft is equal to the fundamental frequency of transverse vibration.
g = accelaration due to gravity (9.81 m/s2 ). y = static deflection at mass The values for natural frequencies relate to cycle/unit time. The higher harmonic modes are not listed. To obtain values for wn in radians/s multiply values by 2.p. Fundamental Natural Frequencies of Beams (bending) and Shafts (Torsion)Cantilevered Beam 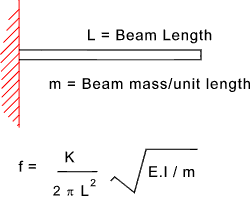
Note: if equation used for whirling speed assume rotating member is supported using "a long bearing /bearing proving substantial angular support e.g. needle bearings" Simply Supported Beam 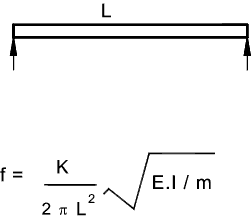
Note: if equation used for whirling speed assume rotating member is supported using "short bearings providing little angular restraint e.g a spherical ball bearing" Beam with fixed ends 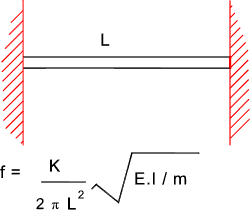
Note: if equation used for whirling speed assume rotating member is supported using "a long bearing /bearing proving substantial angular support e.g. needle bearings" Beam with one end fixed and one end Simply Supported 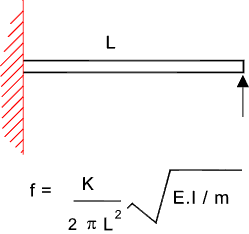
Note: if equation used for whirling speed assume rotating member is supported using "a long bearing /bearing proving substantial angular support e.g. needle bearings" and a short bearing providing little angular support e.g a spherical ball bearing Mass on Cantilever beam Note: Assume beam of negligible mass 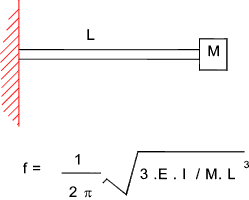 Note: if equation used for whirling speed assume rotating member is supported using "a long bearing /bearing proving substantial angular support e.g. needle bearings" Central mass on Simply supported beam Note: Assume beam of negligible mass 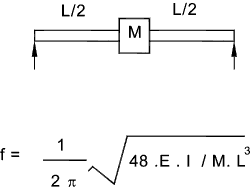 Note: if equation used for whirling speed assume rotating member is supported using "short bearings providing little angular restraint e.g a spherical ball bearing" Mass on Simply supported beam. Off-Centre Note: Assume beam of negligible mass 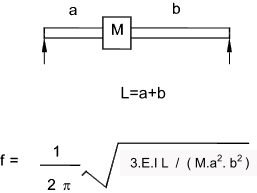 Note: if equation used for whirling speed assume rotating member is supported using "short bearings providing little angular restraint e.g a spherical ball bearing" Mass on beam fixed at bot ends. Mass central Note: Assume beam of negligible mass 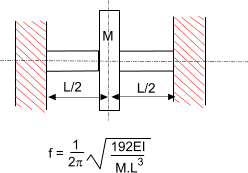 Note: if equation used for whirling speed assume rotating member is supported using "longt bearings providing full angular restraint e.g needle bearings" Multiple Mass on beam 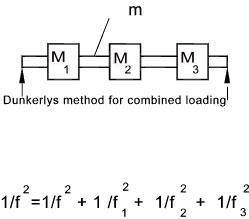 Note: if equation used for whirling speed assume rotating member is supported using "short bearings providing little angular restraint e.g a spherical ball bearing" Formula for Combined Loading 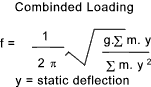 Mass on Cantilevered Shaft In Torsion The following two examples identify the natural torsional frequency of shafts with heavy disks on the ends. Note: Assume shaft of negligible mass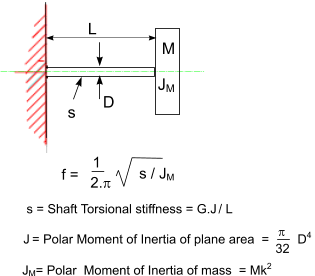 Shaft with mass at both ends Note: Assume shaft of negligible mass 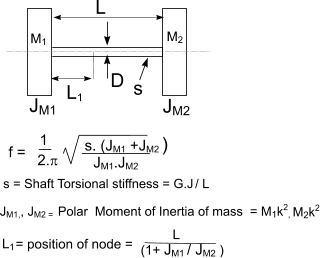 Whirling of shafts When a shaft rotates at a speed equal to the natural frequency of traverse vibration, it results in vibratons at this frequency which becomes large and this is identified as shaft whirling. This also occurs at multiples of the resonant frequency......It must be noted that a Perfectly balanced shaft will not whirl at any speed Additional notes on this topic are found at Natural Frequencies to Traverse Vibrations- Whirling
|
Links to shaft Vibrations
|
|