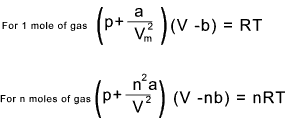Introduction
This page relates to the physical properties of real gases. The webpage
Gas Properties includes some general
physical properties of selected gases. Thermodynamic and heat transfer relationships for fluids can be found on page
Thermodynamics /Heat Transfer
The laws and rules for ideal gases are only reasonable accurate for gases at low pressures
and moderately high temperatures...At pressures around 1 bara or less the ideal gases are
generally reasonably accurate for real gases.
The main reasons for the divergence from the ideal gas laws are that molecules actually
attract each other and that molecules have real volumes. The ideal gas laws
assume that the volume of a gas molecule can be discounted and that molecules do not
attract each other. It is also apparent that as molecules approach very close,
the attraction changes to repulsion.. In 1873 van der Waals devised a crude simple equation
to adapt the ideal gas laws to the behaviour or real gases
Van der Waals Equation
Considering a molecule in a container. The molecule will be attracted to
all other molecules when located in away from the container wall. When local
to the container wall there will be greater attraction towards the molecules within
the centre of the container and its momentum will be reduced. The higher the
pressure greater the inward attract and the more significant is this effect.
The correction for pressure will depend on the number of molecules at the surface and
the number within the body of the gas. Both of these factors vary inversely with
the volume V. Van der Walls proposed that a compensatory factor a/V2 be
added to the true pressure.
It is also true that the volume containing a gas within which the molecules are moving
is reduced by the effective volume of the molecules. This reduction is greater
if the pressure is increased..Van der Walls proposed a factor b to allow for this reduction this
factor is greater at higher pressures.
The Gas law as modified by Van der Waals for real gases is as follows >
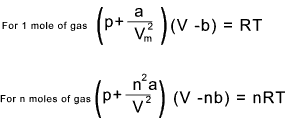
Typical units are as follows
- p = Pressure = Atm or Pa (N/m 2)
- V = Volume = liter or m 3
- Vm = volume of one l mole (litres) or volume of 1 kMole ( m 3)
- T = Absolute Pressure = deg Kelvin
- R = Universal Gas Constant = 8,314 J /mole.K or 8 314 J /kmole.K ( "," is my decimal point)
- n = Number of moles (kmoles)
|
Table of Van Der Waals Constants
| Substance | a | b | |
Substance | a | b |
liter2.atm./mole2
(m3)2.Pa./kmole2 | litre/mole=
m3/kmole |
liter2.atm./mole2
(m3)2.Pa./kmole2 | litre/mole=
m3/kmole |
| Hydrogen | 0,245
2,48x104 | 2,67x 10-2 |
Hydrogen Chloride | 3,8
3,85x105 | 4,1x 10-2 |
| Helium | 0,034
3.44x103 | 2,36x 10-2 |
Ammonia | 4,0
4,05x105 | 3,6x 10-2 |
| Nitrogen | 1,380
1,4x105 | 3,94x 10-2 |
Acetylene | 4,4
4,46x105 | 5,1x 10-2 |
| Oxygen | 1,32
1,34x105 | 3,12x 10-2 |
Ethylene | 4,5
4,56x105 | 5,6x 10-2 |
| Carbon Monxide | 1,491
1,51x105 | 4,00x 10-2 |
Chlorine | 5,5
5,57x105 | 4,9x 10-2 |
| Carbon Dioxide | 3,60
3,65x105 | 4,28x 10-2 |
Sulfur Dioxide | 6,7
6,79x105 | 5,6x 10-2 |
Critical Temperature
The critical temperature for a matter is the maximum temperature that a gas can be liquified
is called the critical temperature for the gas. The liquid state cannot exist above this temperature.
The pressure to cause liquifaction at this temperature is called the critical pressure.
A vapor is really a gaseous state of a substance when its temperature is below the critical
temperature. A vapour can therefore by condensed to a liquid by increasing the pressure.
| Substance | Critical Temp | Critical Pressure | |
Substance | Critical Temp | Critical Pressure |
| Deg. K | atm |
Deg. K | atm |
| He | 5,2 | 2,26 |
H2S | 373,5 | 89,0 |
| H2 | 33,2 | 12,8 |
NH3 | 406,0 | 112,3 |
| N2 | 126,0 | 33,5 |
Cl2 | 417,1 | 76,1 |
| CO | 133,6 | 35,5 |
SO2 | 430,3 | 77,6 |
| O2 | 154,3 | 49,7 |
CCl4 | 556,2 | 45,0 |
| CO2 | 304,2 | 73,0 |
C6H6 | 561,6 | 47,9 |
| HCl | 324,1 | 81,5 |
H2O | 647,3 | 217,7 |
|