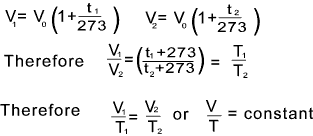Gases
Boyle's Law
When the pressure on a gas is increased at constant temperature the volume
decreases. At constant temperature the volume of a fixed mass of
gas is inversely proportional to the pressure.
PV = constant...At constant temperature
P = the pressure
V = volume of fixed mass of gas
Charles Law.. (Gay-Lussac's Law)
The volume of gas at constant pressure increases by the same relative amount
for every degree rise in temperature.
Vt = Vo +
α v.V o.t = V o (1 + α v. t) ... At constant pressure
α v= coefficient of expansion (theoretically same for all gases )
Vo = Volume of gas at O o (C or F )
Vt = Volume of gas at t o (C or F )
t = Temperature (Degrees Centigrade /Celcius )
If the temperature is in degrees C then α = approximately 1/273
Vt = V o (1 + t /273) ... = At constant pressure
The absolute temperature in degrees Kelvin (K) = the temperature t + 273 Therefore the following relationship holds..
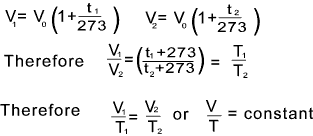
These are alternative forms of Gay-Lussac's Law
Equation of State
Gay-Lussac's law and Boyles law can combined to produce an expression which relates pressure, temperature
and volume. This relationship is called the equation of state...
The derivation of the equation of state is as follows;
A gas has a volume V1 at a pressure of P1 and a temperature T1
If the pressure is changed to P2 and the temperature is T2 and the volume
resulting is V2. The relationship is derived as follows:..
a) The temperature is maintained at T1 while the pressure is changed from P1 to P2
The volume is changed from V1 ' according to Boyle's law as follows...
P1V1 = P2V1 ' therefore V1 ' = P1V1 /P2
b) The pressure is now maintained constant and the temperature is changed from T1 to T2 . The volume will then
change from V1 ' to V2. applying Gay-Lussacs' equation.

The resulting general case of the equation of state for a given mass of gas is...
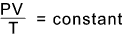
Avogadro's Law
Equal volumes of all gases at the same temperature and pressure contain the same number of molecules...
This law simple states that equal numbers of molecules of different gases occupy the same volume at a given
temperature and pressure... The constant in the above equation will be independent of the gas providing equal
numbers of molecules are involved. This constant is known as the gas constant (R).
This provides the basis for the general equation of state for any gas..
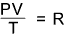
the volume V is the volume occupied by one mole i.e the molar volume at the temperature T and pressure P.
Note:
A mole is that amount of substance which contains as many elementary particles as
there are atoms in 12 gms of carbon 12. (a kmole has as many particles as 12kg of carbon 12 ).
The molar mass of (M) of a substance is the mass of 1 mole of the substance.
Ideal Gas Equation..
At a pressure of P and a temperature T the volume of n moles would be n times as great
as for 1 mole; if this volume is v the the gas equation becomes...
Pv = nRT
Various units can be used I have chosen the following units
- P = Pressure = (Pa) N/m 2
- v = Volume = m 3
- T = Absolute Pressure = deg Kelvin
- R = Universal Gas Constant = 8,314 J /mole.K = 8 314 J /kmole.K
- n = Number of moles
|
The laws and rules for ideal gases are only reasonable accurate for gases at low pressures and moderately high temperatures...At pressures around 1 bara or less the ideal gases are generally reasonably accurate for real gases.
Example: If we had 1.0 mole of gas at 1.0 atm of pressure at 0oC (273.15 K) (STP),
what would be the volume? .....1 Atm = 101 325 Pa. (N/m 2 )
( I use "," as decimal place, "." as multiply symbol, " " for thousands)
(1 . 8,314 . 273,15) / 101 325 = 0.02214 m 3 = 22.14 litres
The molar volume of any ideal gas is 22.14 liters at STP
If this was hydrogen H2 with M = molar mass = 2 grammes then the density = 2/22,14 = 0,09 gm/litre ( kg/m 2)
Dalton's Law of Partial Pressures
This law establishes a connection between the total pressure exerted by the mixture
of a number of gases and the pressure exerted by each separate gas. Dalton's law states .
The partial pressure of each gas in a mixture is defined as the pressure the gas would exert
if it alone occupied the whole volume of the mixture at the same temperature.
If a vessel of volume contains two gases n1 moles of gas 1 and n2 moles of gas 2.
If the vessel were only filled with n1 moles of gas 1 the resulting pressure would be p1.
In a similar manner if the vessel were only filled with n2 moles of gas 2 the
resulting pressure would be p2. All the above are considered to be at the
same temperature.
The pressure when the two gases are present = P. Thge law of partial pressures states
P = p1 + p2
This applies to any number of ideal gases...
Developing this relationship further and writing the ideal gas equation for each gas occupying
the vessel on its own.
p1 v = n1 RT
p2 v = n2 RT etc..
Hence (p1 + p2 ) v = (n1 + n2 )RT
Therefore Pv = (n1 +n2 )RT
If n = (n1 + n2 ) = total number of moles in a gas mixture it can
be easily proved that
p1 = (n1 / n ).P
If the mole fraction of any gas in a mixture is identified as x a then p a = x a.P
Graham's Law of Diffusion
Diffusion is the tendency for any substance to spread uniformly to fill the space available
to it. This tendency is apparent primarily for gases but it is also exhibited by
liquids and solids to much lesser extents... If two vessels containing to different
gases are connected then , whatever the orientation of the vessels the gases will, after a short time
peiod each be spread uniformly throughout the jars. The effects of gravity have
very little effect on this process.
It the gas molecules are small enough i.e hydrogen and helium. The gas may even spread
out through the containing vessel wall. Gases contained in porous earthernware vessel
diffuse out into the environment and surrounding gases diffuse in...
When gases diffuse through fine pores and holes the process is often termed "effusion".
Grahams law is another ideal gas law which is only approximate states:
The rate of diffusion (or effusion) of a gas is inversely proportional to the square root of its density
If d1 and d2 are the densities of two gases and M1 and M2 are the
associated molecular weights and R1 and R2 are the respective rates of effusion and k is a proportionality constant...
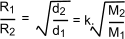
Kinetic Theory of Gases
This generally accepted theory provides a close agreement with experimental data
of ideal gases under conditions of high temperature and low pressures . This theory is based
on the following postulates.
- A gas is composed of molecules which can be considered as identical, hard smooth spheres
- The molecules are perfectly elastic with no loss of energy on impacts with other molecules
- The diameter of the molecules is small compared to the distance moved between impacts,
- The volume of the molecules is small compared to the volume of the gas
- The molecules are in complete random motion , impacting with other molecules and the containing walls
- The time of the impacts is small compared with the time of free motion
- Attractive and repulsive forces between the molecules are negligible
- The average kinetic energy of the molecules is proportional to the absolute temperature
- The pressure generated by the gas results from the impact of the molecules upon the containing walls
|
Derivations from kinetic Theory
The following notes are in the mks system not the cgs system as is normally used for
consideration of molecules...
The derivations illustrated are all approximate but they provide reasonable correct results
for ideal gases following the rules relating to the kinetic theory..
Pressure
Consider a cube of sides 'l' aligned in the x, y and z. The cube is full of "n"
molecules each with a mass "m". The pressure results from the impact of the molecules on the walls of
the cube.
Each molecule is moving with a velocity c which has components u,v,w in the x,y and z directions
respectively. c 2 = u 2 + v 2 +w 2
Considering the component of the motion of 1 molecule in the x direction. The molecule
impacts with the wall normal to its direction of motion and rebounds with a velocity -u.
The change of momentum is from mu to -mu = 2mu. The motion then continues and the
molecule hits the opposite wall after a period l/u. The rate of change of momentum
of the molecule is therefore 2mu.u/l = 2mu 2 / l (kg.m/s 2 ).
Likewise rate of change of momentum in the y direction = 2mv 2 /l (kg.m/s 2
and in the z direction is 2mw 2 /l (kg.m/s 2...
Newtons law states that the rate of change of momentum is equal to the force acting. Therefore
the total force due to the impacts of a single molecule =
F = 2 mc 2 / l = 2m (u 2 + v 2 + w 2 ) / l
There are n molecules in the cube each molecule exerting a similar force. The total force resulting
from n molecules is therefore .
Ft = 2 m (c1 2 + c2 2 + c3 2
...+ cn 2) / l
The mean square velocity c is the average of the squares of the velocities of n molecules is defined
as follows.
c = (c1 2 + c2 2 + c3 2
...+ cn 2) / n
The total force of n molecules is therefore
Ft =2nmc 2 / l (Newtons)
Pressure is defined as the pressure per unit area and the area of the walls of the cube
is 6 l 2. Therefore the resulting pressure =
P =2nmc 2 / (l 6 l 2) = nmc 2 / 3.v .....A
Boyle's Law
J.C. Maxwell (1860) arrived at the conclusion that the mean kinetic energy of the molecules
of all gases are the same at constant temperature.
At a constant temperature the kinetic energy mc2 /2 is constant for any gas.
For a fixed mass the number of molecules remains the same and therefore mc2 /2 will be constant.
equation A above can be rewritten as
Pv = nmc 2 / 3 .....Equation B
It is clear from the above notes that at constant temperature the right side of the equation
is constant
Pv = Constant
This is in accordance with Boyle's law...
Avogadro's Law
Also following form the equations above
P1v1 = n1m1c1 2 / 3..... and.... P2v2 = n2m2c2 2 / 3
Now if P1 = P2 and v1 = v2 Then
n1m1c1 2 / 3 = n2m2c2 2 / 3
If the gases are at the same temperature then the kinetic energies are the same
m1c12 /2 = m2c22 /2
and therefore
n1 = n2
That is two gases at the same pressure and temperature occupying the same volume contain
the same number of molecules.. The agrees with Avogadro's law,
Charles's Law
It is postulated above that the temperature T is proportional to the mean kinetic
energy of a gas and therefore from equation
B above it follows that
Pv = nkT where k is a proportionality constant that is is equal
for all gases. From Maxwells proof that the kinetic energy of all gases is equal
at the same temperature it is concluded that k is a universal constant for all gases. If the pressure
is held constant then it is clear from the equation above
v/T = constant
This conclusion agrees the Charles Law (Gay-Lussac's law).... The absolute temperate scale
is the same as the temperature defined in reference to the mean kinetic energy of the molecules
in an ideal gas
|