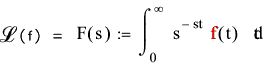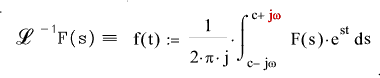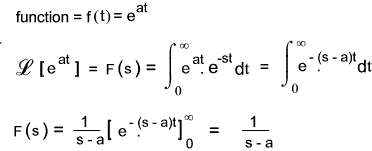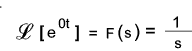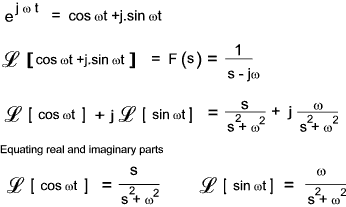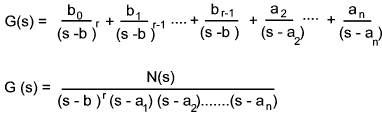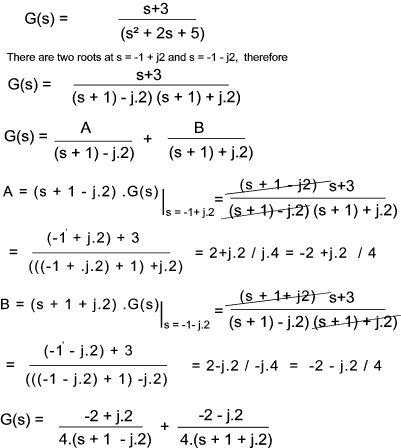Introduction
In control system design it is necessary, to analyse the performance and stability
of a proposed system before it is built or implemented. Many analysis
techniques use transformed variables to facilitate mathematical treatment of the problem. In
the analysis of continuous time dynamical systems, this generally involves the use of Laplace Transforms
Applying Laplace Transforms is analogous to using logarithms to simplify certain types of
mathematical operations. By taking logarithms, numbers are transformed
into powers of 10 or e (natural logarithms ). As a result of the
transformations, mathematical multiplications and divisions are replaced by additions and
subtractions respectively. Similarly, the application of Laplace Transforms to the analysis of
systems which can be described by linear, ordinary time differential equations overcomes
some of the complexities encountered in the time-domain solution of such equations.
Laplace Transforms are used to convert time domain relationships to a set of equations
expressed in terms of the Laplace operator 's'. Thereafter, the solution of the original problem
is effected by simple algebraic manipulations in the 's' or Laplace domain rather than the time
domain.
The Laplace Transform of a time variable f(t) is arrived at by multiplying f(t) by
e -st and integrating from 0 to infinity..
f(t) must be a given function which is defined for all positive values of t.
s is a complex variable defined by... s = a +jω and j = sqrt (-1).
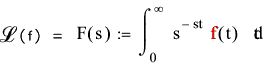
A table of laplace transforms is available to transform real time domain variables to
laplace transforms. The necessary operations are carried out and the laplace transforms obtained
in terms of s are then inverted from the s domain to the time (t) domain. This tranformation
from the s to the t domain is called the inverse transform...
The contour integral which defines the inverse Laplace
Transform is shown below... for reference only, for in practice, this integral is
seldom used as table lookup are generally all the operations required for the inverse
transform procedure..
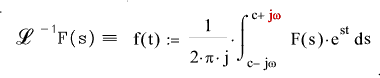
Laplace Transform Operations.
| Operation | f(t) | F(s) |
| Linearity |
x 1 f 1 (t) + x 2 f 2 (t) |
x 1 F 1 (s) + x 2 F 2 (s) |
| Constant Multiplication |
a.f(t) |
a.F(s) |
| Complex shift Theorem |
e ± a.t.f(t) |
F(s  a.t ) a.t ) |
| Real shift Theorem |
f( t - T ) |
e -Ts F(s) for (T >= 0 ) |
| Scaling Theorem |
f( t / a ) |
a F(as) |
| First Derivative |
f' (t) |
sF(s) - f(0+) |
| 2nd Derivative |
f'' (t) |
s 2 (F(s) - sf(0+) - f'(0+) |
| 3rd Derivative |
f''' (t) |
s 3 (F(s) - s 2. f(0+) - s.f'(0+) - f''(0+) |
| 4th 5th .. Derivative follow principles established above |
| First Integral |
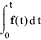 |
(1/s).F.(s) |
| Convolution Integral |
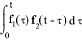 |
F 1(s). F 2(s) |
Table showing selection of Laplace Transforms.
| Laplace Transforms |
| | |
| No | Time Function = f(t) | Laplace Transform = F(s) |
| 1 | d ( t )..Unit impulse | 1 |
| 2 | d(t - T)..Delayed impulse | e -Ts |
| 3 | t ...Unit ramp | 1 / s 2 |
| 4 | t n | n ! / s ( n+1 ) |
| 5 | e - at | 1 / ( s + a ) |
| 6 | e at | 1 / ( s - a ) |
| 7 | (1 / a) .(1 - e -at ) | 1 / {s.( s + a )} |
| 8 | (t n / n !)e - at |
1 /(s + a ) n - 1...n = 1,2,3,4,... |
| 9 | sin ωt |
ω / (s 2 + ω 2 ) |
| 10 | cos ωt |
s / (s 2 + ω 2 ) |
| 11 | 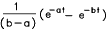 |
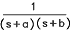 |
| 12 | 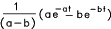 |
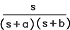 |
| 13 | (1 / ω 2) .(1 — cos ωt ) |
1 / {s.( s 2 + ω 2 )} |
| 14 | (1 / a 2) .(a.t — 1 + e -at ) |
1 / {s 2.( s + a )} |
| 15 | 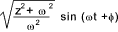 |
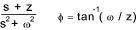 |
| 16 | 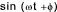 | 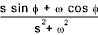 |
| 17 | u(t) or 1 ...Unit step | 1/s |
| 18 | u(t - T)...Delayed step | ( 1 / s )e -Ts |
| 19 | u(t) - u(t - T) or 1 ...Rectangular Pulse | ( 1 / s ) (1- e -Ts ) |
| 21 | e — at cos ωt | (s+a) / { (s+a) 2 + ω 2 } |
| 22 | (1 / a 2 )(1 — e -at — ate -at ) | (1 / s) ( s + a) 2 |
| 23 | 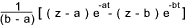 | 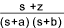 |
| 24 | 1 / [( s + a ) 2 + ω 2 ] | (1/ω).e -at sin ωt |
| 25 | 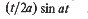 | 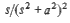 |
| 26 | 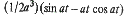 | 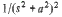 |
Derivation of table values
examples on how the table values have been derived are provided below.
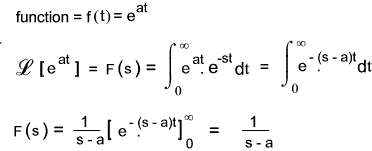
From above the transform for a unit step i.e f(1) is easily obtained by setting
a = 0 ( e 0.t) = 1)
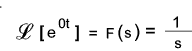
From above the transform for cos ωt and sin ωt is
obtained by setting a = jω
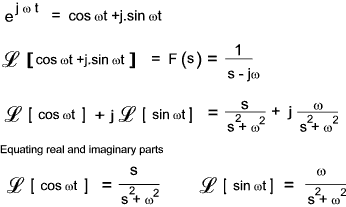
Laplace transform example
An example of using Laplace transforms is provided below

The manipulation of the laplace tranform equation into a form
to enable a convenient inverse transform often involves use of partial fractions...
Partial Fraction Expansion...Notes are also provided for partial fractions on webpage Partial Fractions
The splitting up of a ratio of polynomials is often necessary to produce simpler ratios
from which inverse Laplace transforms are more conveniently obtained. The most favoured
procedure for converting using hands-on (as opposed to using computers) is the "Heaviside
cover up" procedure..
An example application including partial fraction expansion is as follows.....

Partial Fraction Expansion process using the Heaviside cover up method
The Laplace operations generally result in a ratio
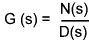
This must be proper in that the order of the denominator D(s) must be higher than the numerator N(s).
If the function is not proper then the numerator N(s) must be divided by the denominator using the long division method.
The next step is to factor D(s)
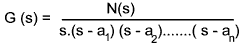
a 1,a 1 etc are the roots of D(s).
D(s) is then rewritten in partial fraction form..
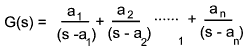
To obtain a 1 simply multiply both sides of the equation by (s - a 1 ) letting s = a 1
This results in all terms on the RHS becoming zero apart from a 1...
G(s).( s-a 1 )| s = a 1 = a 1
The LHS is multiplied be (s - a 1) thus cancelling out (s - a 1)in the denominator. ...
and all instances of s are then replaced by a 1
Note: If one of the terms in the numerator is s then this is simply equivalent to (s- a x) with a x = 0.
Repeated Roots....
When the denominator has repeated roots the breakdown into partial fractions is treated differently
as shown below...
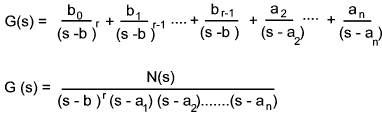
The factor b 0 is obtained in exactly the same way as above..
The factor b 1 is obtained by first differentiating G(s).(s-b) with
respect to ds and then substituting s with b as before.
This will generally involve the differentiation d(u/v) = (vdu - udv)/v 2..
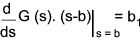
The factors b 2 to b r is obtained by progressive differentiation
of G(s)(s-b) and dividing the result by the factorial of the level of
differentiation (if d/ds 2 then divide by 2!, if , d/ds 3 then divide by 3!(6))...
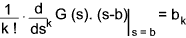
Complex Roots....
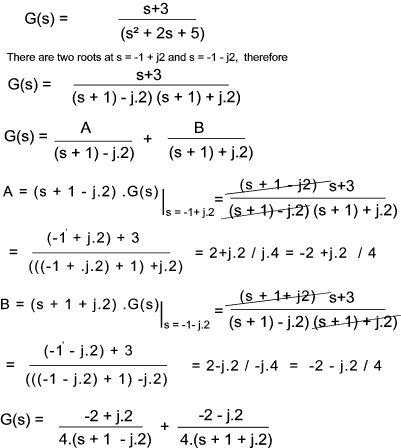
|