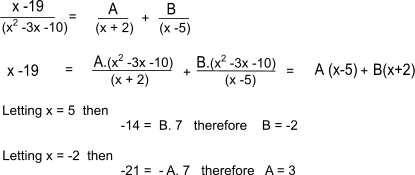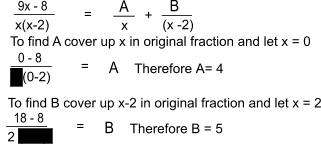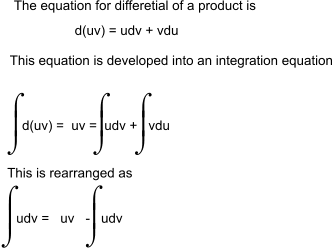
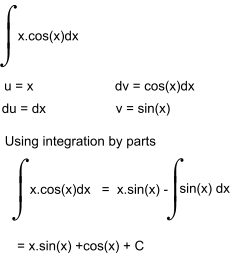
Integration by parts is a technique for performing integration by expanding the differential of a product of functions and expressing the original integral in terms of a known integral .

A simple example illustrates the method of Integration by parts.
The requirement is to integrate the product x.cos(x)dx

A complicated algebraic fraction can often be reduced to to its equivalent partial fractions such that it allows an integration process to be simplified.    A typical example is shown below

Rules for Partial fractions

A simple example of the application of these rules is as follows

The equations are solved for A and B as follows

A second example is provide below

Partial Fractions -Cover up rule

There are many simple cases where the cover up method can be used . This method only applies if the denominator of the original fraction has non-repeated , linear factors. The method is illustrated by the following example.