Pumps

Pump notes

Table showing generic pump types

Note: Links to more detailed information are included in the rows below..

Pumps
Kinetic		Positive Displacement
Peripheral-link	Rotodynamic-link	Reciprocating-link		Rotary Positive Displacement-link
	Radial Flow	Diaphragm	Plunger	Single Rotor	Multiple Rotor
	Axial Flow			Sliding Vane	Gear
	Mixed Flow			Flexible Vane	Screw
				Mono	Lobe
				Peristaltic
				Piston

Single Pump Systems

The system head generally consists of two parts:-

Static Head

The difference between the suction and final discharge static levels in an open system. This is usually independent of flow.

Energy Loss in the Pipework.

This is essentially the friction head loss in the piping and is related to the flow . Under turbulent flow operating conditions the friction loss may be assumed to be related to the flow velocity ². Therefore a friction loss plot is a parabola passing through the origin.

The system characteristic curve is generally drawn as the parabolic friction loss curve superimposed on the constant head line.

Methods of Calculating the Head Loss are found on this site Head Loss Calculations

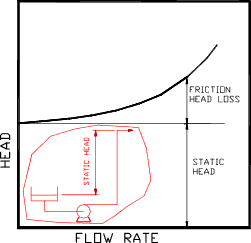
It is often the case that the static head is small compared to the friction loss e.g. in close circuits.

For some systems the static head is important only for comparatively short periods when the system is filled with the liquid. These are circuits where the piping rises and then falls to the same, or lower level compared to the pump level. It is possible that if the final liquid outlet level is below the pump level then a syphon is generated and the static head assists the pump in overcoming the friction losses.

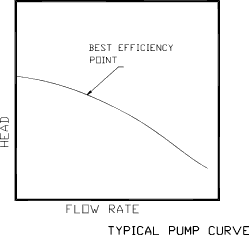
Centrifugal pump curve.

A typical pump operating with a set impeller diameter and at a set rotational speed delivers a head related to the liquid flow rate. The head is normally highest when no flow is delivered (dead headed) and lowest when there is no restriction to the flow and it is consequently at its maximum flow. Both these extreme conditions are very undesirable. A dead headed pump will result in all of the energy supplied at the pump shaft being dissipated in the small closed volume of liquid. -The fluid will rapidly heat up An open discharge pump is operating with very poor efficiency with a risk of overloading the drive motor.

A typical motor characteristic curve is shown below.

A pump is generally selected for a duty such that when the pump curve is superimposed on the system characteristic curve the curves cross over at the pump best efficiency point (BEP) at the desired flow rate.

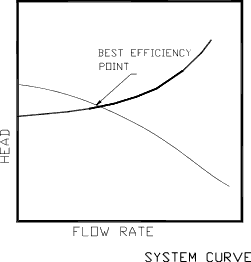
It is impractical to obtain a perfect match of the best efficiency point of the pump with the system characteristic curve and generally the flow will be higher or lower than desired. This may result in the pump not providing the desired performance and may sometimes result in pump instability. Methods of achieving a match include:

Adjusting the pump speed
Adjusting the pump impeller diameter
Changing the impeller design
Adjusting the system resistance
Modifying static head
Providing a system bypass flow route

There is a modern trend to provide electrical variable speed drives to pump to enable the performance of the pump to be adjusted - on the run. The modern AC inverter controlled motor is a very efficient low cost method of varying the motor speed.

Multi-Pump Systems

Centrifugal pumps in parallel provide additive flow conditions and when mounted in series provide additive head conditions. Therefore three matched pumps mounted in series will provide the same flow at three times the head (aprox.) compared to one pump. Three matched pumps in parallel will provide the same head at three times the flow compared to one pump. A very popular variation on this theme is to provide multi-stage pumps with up to twenty stages mounted on a common shaft to provide a high head from a single pump.

Head

The energy imparted to a fluid by a pump is measured as the head (in metres)per unit weight of fluid.

dH = (Z₂ - Z₁) + ( P₂ -P₁ )/ (ρ g ) - (v₂² -v₁²)/ (2 g )

dH = Fluid Head developed across pump ..m
Z₁ = Fluid Supply Level..m
Z₂ = Fluid Discharge Level..m
P₁ =Pressure over Supply Fluid..N/m²
P₂ =Pressure into which fluid is discharged ..N/m²
ρ = Fluid Density..kg/m³)
g = Accelaration due to gravity 9.81 m / s²
v₁² Fluid velocity at pump inlet m/s
v₂² Fluid velocity at pump discharge m/s

Normally the velocity head and the height head is ignored for initial selection of the pump.

The head developed is therefore approximated to the static pressure difference expressed as a column of the liquid pumped in metres of fluid.

Note: For accurate calculations the difference in height of the pump suction and out discharge flanges and the difference in velocity head should be considered.

To convert the differential head developed to pressure difference in N/m²

p (N/m² ) = dH * ρ g

NPSH

As liquid flows from the pump inlet flange into the energy conversion region e.g.impellor or piston chamber, the head initially falls as the velocity of the fluid is increased. If the liquid is near its vapour pressure the drop in head may be sufficient to cause the liquid to boil. This results in "cavitation". Cavitation is detectable as a rattling noise and results in low efficiency, and high risk of damage to the pump.

The head drop for any pump design at a selected flow is provided by the manufacturer as the NPSH required NPSHR measured in metres of fluid pumped.

If the head of the fluid at the pump suction flange is not greater that the vapour pressure, at the pumping temperature, plus the NPSHR then cavitation will occur.

The head at the pump inlet flange - the relevant vapour is called the NPSH available NPSHA.

The NPSHA must be at least 1-2m of fluid greater than the NPSHR to avoid cavitation.

Pi = Surface pressure of fluid (N/m²)
Pb = Barometric pressure (N/m²)
Pv = Vapour pressure of fluid (N/m²)
ρ = Fluid density (kg/m³)
Ve = Velocity of fluid at pump inlet (m/s)
Ze = Fluid Surface level above pump inlet. (m)
Fe = Friction loss is pipe to pump. (m)

Methods of Calculating the fluid friction loss are found on this website Pipe Flow

Note: 1 bar = 10⁵ N/m²

Pumps

Pump notes

Pages in this section