| |
Fluids Index Fluid Flow in pipes
Pump Notes and Calculations Pumps
Valve Notes Valves
Fluid Power Notes Pneumatics .....
Hydrostatics
Introduction.....
Symbols.....
Fluid Flow.....
Modified Bernoulli's Equation.....
Pipe Flow Calculations.....
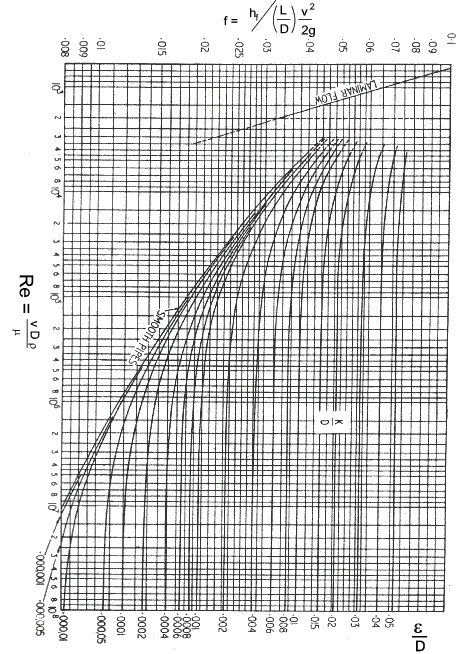
Moody chart.....
Pipe roughness values.....
L/D values for fittings.....
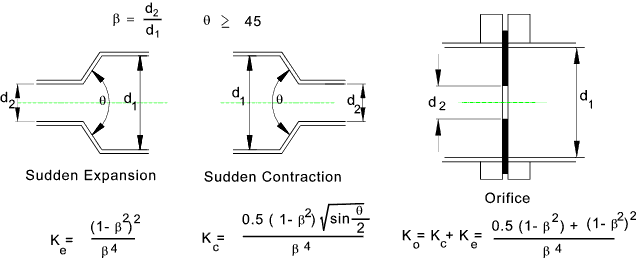
K values for Sudden Expansion -Contraction & Orifice.....
Pipe flow velocities.....
|
Introduction The following notes should enable a mechanical engineer to establish basic flow conditions and head losses along pipe routes in which fluids are flowing. The equations are most relevant to liquids although approximate sizing for gases can be carried out if appropriate correction factors are used,where necessary, and low gas velocities are considered. Symbols
Fluid Flow Fluid flowing in pipes has two primary flow patterns. It can be either laminar when all of the fluid particles flow in parallel lines at even velocities and it can be turbulent when the fluid particles have a random motion interposed on an average flow in the general direction of flow. There is also a critical zone when the flow can be either laminar or turbulent or a mixture. It has been proved experimentally by Osborne Reynolds that the nature of flow depends on the mean flow velocity (v), the pipe diameter (D), the density (ρ) and the fluid viscosity Fluid Viscosity( μ). A dimensionless variable for the called the Reynolds number which is simply a ratio of the fluid dynamic forces and the fluid viscous forces , is used to determine what flow pattern will occur. The equation for the Reynold Number is
For normal engineering calculations , the flow in pipes is considered laminar if the
relevant Reynolds number is less than 2000, and it is turbulent if the Reynolds number is greater than
4000. Between these two values there is the critical zone in which the flow can be either laminar or turbulent
or the flow can change between the patterns... Steady Flow Equation.... Reference :
The steady flow equation steady flow equation (energy per unit mass ) for a system is identified below...
If q = w = 0 and the fluid is incompressible and frictionless
and if the variables are converted to measured heads of the fluid , that is the units are per
unit weight (ρg) - then the Bernoulli's equation results ..
In real flow systems there are losses due to internal and wall friction which result in increase in the internal energy of the fluid. (q > 0). Reference Bernoulli's Equation real Fluids . The bernoulli equation is modified to reflect these losses by adding a term h f = Head loss due to friction.= (u2 -u1 - q) The modified bernoullis equation is therefore ..
The object of most pipe flow head loss calculations is to determine the friction head loss and allow estimation of the pump /compressor power required to pump the fluid along the piping. In most fluid transfer cases the fluid is a incompressible (a liquid) and the flow rate (Q) is constant along the pipe run and therefore the velocity at any point can easily be calculated. The head (z) can also be easily obtained from the pipeline geometry. The system pressure and head loss are therefore the variables generally subject to the detailed pipeline calculations.... Pipe Flow Calculations In determining the head loss (pressure drop) along a pipe as
a result of friction losses it is first necessary to determine the following:
Consistent units to be used i.e Typically ρ = kg/m3,
v = m/s, D= m, μ = Ns/m2
( 1 Ns/m2 = 103cP)
The head loss along the pipe can now be calculated using the Darcy-Weisbach equation
The result of the calculation is in units of head of the fluid. . It is based on the pipe being all one dia and the fluid is incompressible For a single pipe line with a number of fittings the total head loss is calculated as
K p = f (L/D) for the length of pipe. ( this may be made up of ∑ f(L/D). for a number of different pipe lengths of different diameters ) A Moody chart (see below) is used to determine the turbulent flow friction factor from the Reynolds number and
the relative roughness of the pipe. If the flow is laminar then the fricton factor is 64/Re.
Note: it is suggested that for laminar flow in pipe at Re number approaching 2000 the above K values are used for bends and fitting with reasonable accuracy A moody chart and tables for roughness values and (L/D) factors for various fittings are provided below Moody Chart
Various typical values of hydraulic roughness (ε) Note:
Typical Values of L/D for Fittings The losses through fittings are generally evaluated by obtaining K = fT(L/D) Table of pipe friction values for clean pipe in region of complete turbulence
The K180 value for a 180o bend may be derived from the equivalent K90 which is calculated from the above tables using the equation The K180 = 0,25.π.fT . r/D + 1,5.K90
For laminar fluids with low Re numbers ( "<" 500) the K values obtained using the above are probably very innaccurate. The table below illustrates how this affects the K values
K values for Sudden Expansion-Contraction & Orifice The losses through these fitting are generally evaluated by
first obtaining β = d2 / d1
Reasonable Velocities of fluid in Pipes
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Useful Links
|
|
Fluids Index