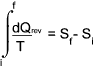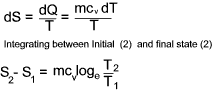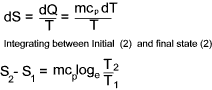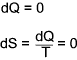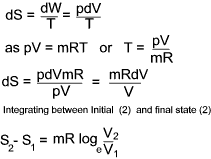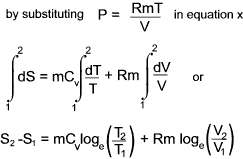Introduction
Entropy is a measure of the quality of energy and how usable it is....
Entropy (S)is very difficult to visualise because it does not represent anything tangible.
The entropy increase δS is the heat transfer to a substance δQ divided by the absolute
temperature of the substance (T) during a reversible heat-transfer process.
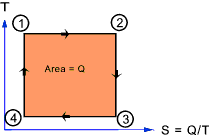
At the very simplest level , on a plot of Absolute Temperature (T) against Entropy
(Q/T = S) for a reversible cyclic process (as shown below) the area enclosed = Q
Note: The reversible cyclic process shown below is actually the theoretical Carnot cycle.
1->2 being isothermal expansion.
2->3 being adiabetic expansion.
3->4 being isothermal compression.
4->1 being adiabetic compression.
The change in entropy ( δS ) of a substance is that quantity which when multiplied
by the absolute temperature at which the change took place results in the amount of energy ( δQ )
flow reversibly by heat transfer across the boundary enclosing the substance.
Total entropy is a property (extensive) of a substance and therefore the change in entropy
during a process, from an initial to a final state, is the same whatever the path taken. The change in entropy resulting from
any real (irreversible) process is the same as that resulting from a reversible process with
the same initial and final states. Therefore to determine the change in entropy
resulting from a real irreversible process an equivalent reversible process must be
envisaged to replace the real process from initial to final states before integration of the following
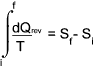
Typical SI units for total entropy (S) change are kJ /K.
SI units for specific entropy (s) change are kJ/kg.K
Entropy Change for ideal fixed mass closed system gas processed
For an ideal constant volume process... (dQ = mcvdT )
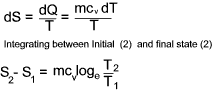
For an ideal constant pressure process... ( dQ = mcpdT )
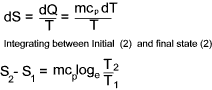
For an ideal adiabetic process...
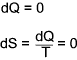
For an ideal isothermal process...
There is no change in temperature and therefore there is no change in internal energy U.
From the first law of thermodynamic dQ = dU + dW. If dU = 0 then dQ = dW.
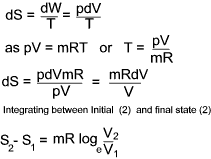
Entropy changes in terms of properties of a perfect gas
From the definition of entropy i.e δQrev = TδS
and from the first law of thermodynamics is dQ = dE + dW which, for a reversible process can be written as
δQrev =δE + PδV...
it can be
deduced that dE = TdS - PdV for a reversible process and if the substance is a gas of mass m then
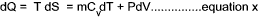
For a perfect gas PV = mRT and assuming Cv is constant.
a) Entropy change in terms of V and T
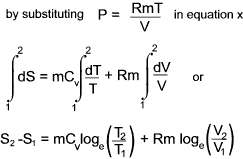
b) Entropy change in terms of P and T
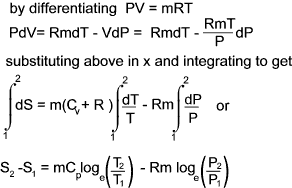
c) Entropy change in terms of P and V

Example ..Entropy Change in Joules Experiment
|
To determine the entropy change in the irreversible adiabetic expansion of Joules
experiment....
-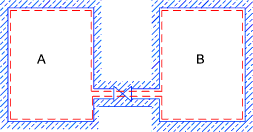
In this experiment a gas at high pressure (properties P1, V1,T )in chamber A which is connected to
a second evacuated chamber B via a valve. When the valve is opened the gas
in chamber A moves by free unresisted expansion into chamber B until the pressures equalise (final properties P2, V2,T ).
The gas is supposed perfect and the temperature does not change (no work has been done). An irreversible
expansion has taken place.
The equipment is so arranged that there is no heat transfer between the surroundings and the system (δQ = 0). Although
δQ = 0 the process is irreversible and therefore δQ is not zero.
To determine the change in entropy the process is replaced by a reversible process which has the same initial and final
conditions i.e. an isothermal process.
For an isothermal process the change in entropy =
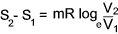
In this case although the process is adiabetic because it is not reversible it is not isentropic. There is
a resulting increase in entropy reflecting the various irreversible energy losses in this process
|
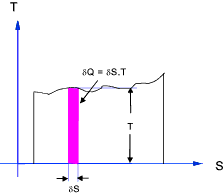
Adiabetic ,Isentropic, and Isothermal Processes - Real and Reversible
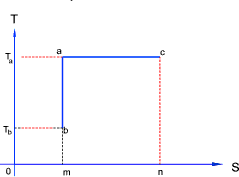
Ideal reversible adiabetic and isothermal processes are straight lines on the TS chart as shown
above ac = ideal isothermal process and ab = ideal isentropic process. An adiabetic process
is one which is insulated against heat transfer and an isentropic process is one with a constant entropy.
δQ may be zero during a adiabetic process but if the process is not reversible then
δS = δQ /T does not apply and δS is not zero.
If the process is reversible then δQ = 0 and δS = 0 i.e the process is adiabetic
and isentropic.
A isentropic process is not necessarily reversible for a real expansion or compression-with all the associated
eddies and friction associated with real processes may have sufficient heat transfer to
maintain the entropy of the relevant substance constant (δS = 0 ). A real process
could be isentropic but would not at the same time be adiabetic because some heat transfer
would be necessary. The following relationships are possible
- In a real (irreversible) adiabetic process δQ = 0 but δS > 0
- In a reversible adiabetic process δQ = 0 and δS =0 0
- In a real (irreversible) isentropic process δS = 0 but δQ < 0
- In a reversible isentropic process δS = 0 and δQ = 0 0
|
|