Introduction
The steady flow energy equation relates to open systems working under steady conditions i.e in which conditions do not change with
time.
The boundary encloses a system through which fluid flows at a constant rate, whilst heat transfer occurs
and external work is done all under steady conditions ,that is , the rates of mass flow
and energy flow are constant with respect to time.
The equation for steady flow ( the steady flow energy equation ) is generally written per unit mass as
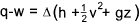
q = heat transfer across boundary per unit mass
w = external work done by system per unit mass
z = fluid height
v = fluid velocity
h = fluid enthalpy ( u (internal energy + pv (pressure.specific volume)
Note in the examples below the system control volumes are defined by the red dashed line.
Heater.. The steady flow equation as applied to a fluid heater..
Potential energy (z) assumed to be constant..
Kinetic energy changes (1 to 2) assumed to be very small
Heater
w = 0 therefore
q = h2-h1
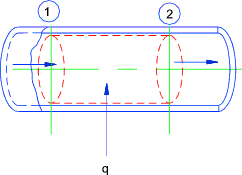
Turbine ..(Assumed Adiabetic Expansion)..The steady flow equation as applied to
a turbine..
Potential energy (z) assumed to be constant..
Kinetic energy changes (1 to 2) assumed to be very small
 Turbine
Turbine
q = 0 therefore
w = h2-h1
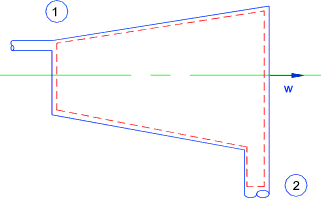
Throttling ..(Assumed Adiabetic )...The steady flow equation as applied to a
orifice..
Potential energy (z) assumed to be constant..
The higher velocity at orifice section is dissipated in tube downstream of the orifice and
therefore the kinetic energies at 1 and 2 are similar
Orifice
q = w = 0 therefore
therefore h1 = h2
Nozzle..(Assumed Adiabetic )...The steady flow equation as applied to
smooth nozzle..
Potential energy (z) assumed to be constant..
Kinetic energy changes are assumed to be significant
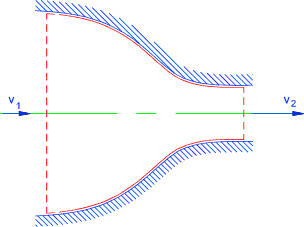
Nozzle
q = w = 0 therefore
(v22 - v12 ) /2 = (h1 - h2 )
| 
 Turbine
Turbine
