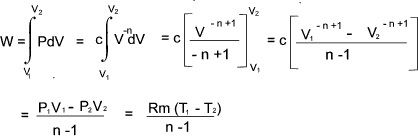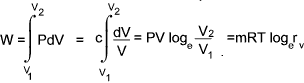Introduction
This page provides a limited notes on thermodynamic relationships useful
to mechanical engineers.
Nomenclature
| Identifier |
Description |
Units (typical) |
| c p |
Specific Heat Capacity at Constant pressure |
kJ/(kg K) |
| c v |
Specific Heat Capacity at Constant Volume |
kJ/(kg K) |
| P |
Absolute Pressure |
N / m 2 |
| T |
Absolute Temperature |
K |
| V |
volume |
m 3 |
| m |
mass |
kg |
| W |
Work Output per unit mass |
kJ/kg |
| M |
Molecular Weight |
- |
| R o |
Universal Gas Constant = 8,31 |
kJ /(kg mole.K) |
| Q |
Heat Quantity |
kJ |
| R |
Gas Constant = R o / M |
kJ /kg.K |
| U |
Internal energy (thermal) |
kJ |
| γ |
Ratio cp / cv |
- |
Thermodynamic Process Relationships
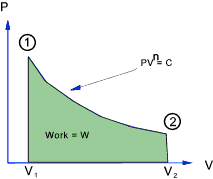
General Polytropic Process
The majority of frictionless processes for ideal gases are called polytropic processes and
are in accordance with the following relationship
PV n = constant
That is PV n = c
therefore P = cV -n
Equation of state for and Ideal Gas
PV = mRT
Thermodynamic Relationships between P,V & T
Consider a piston in a frictionless cylinder
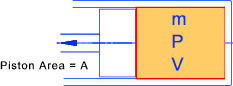
The work done on/by the gas in moving the piston δx =
(PA)δx = P δ V = δ W
The gas is assumed to be expanding in balanced resisted reversible process.
The equation of state for an ideal gas is assumed to apply i.e PV = mRT
The total work done in moving the piston from state 1 to state 2 =
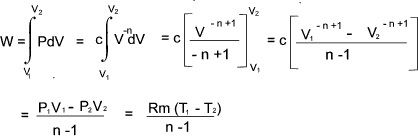
For a perfect gas - The relationship between Temperature , Pressure and Volume over a cycle
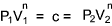

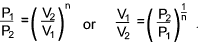
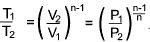
Adiabatic Process.
For an adiabatic process with no transfer of heat across the system boundary.(Q = 0 )
Consider a fixed mass of gas in a cylinder which is expanding in a reversible manner...
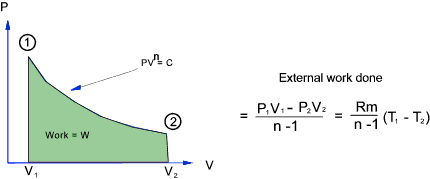
For an adiabatic process there is no heat transfer.
Therefore applying the
first law of thermodynamics ..heat transfer (= 0) = increase in internal energy +external work
done by gas...
Therefore the increase in internal energy = - External work done by gas
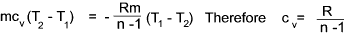
It is shown below that cp - cv = R = cv ( cp / cv -1) and therefore
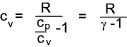
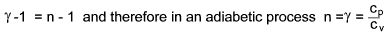
γ = 1.4 for Air, H 2,
O 2, CO, NO, Hcl
γ = 1.3 for CO 2, SO 2,
H 2O, H 2S, N 2O, NH 3, CL 2,
CH 4, C 2H 2, C 2H 4
Isothermal Process
In a isothermal process the temperature = constant and therefore
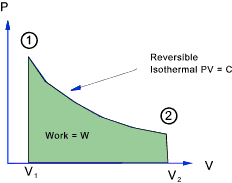
PV = c and P = c / V
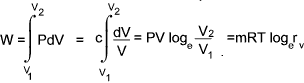
Internal Energy, Cp and Cv
Although it is not possible to determine the absolute value of the internal energy
of a substance. The internal energy change between the initial and final
equilibrium states of any process is definite and determinable.
It can be easily proved that the internal energy of a fluid depends on the temperature
alone and not upon changes in the pressure or volume.
Heating at constant volume....
If a definite mass of gas (m) at constant volume is a closed system is heated from
initial conditions P1, V, T1, U1 to
P2, V , T2,U2. As the volume is fixed then no work
has been done. Then in accordance with the First Law
of Thermodynamics (δQ = δU + δW ).
mCv (T2 - T1) = (U2 - U1) + 0
or U2 - U2 = mCv (T2 - T1)
Heating at constant pressure....
If a definite mass of gas (m) at constant volume is a closed system is heated from
initial conditions P, V1, T1, U1 to
P, V1 , T2,U2. As the volume is fixed then no work
has been done. Then in accordance with the First Law
of Thermodynamics (δQ = δU + δW ).
mcp (T2 - T1)
= (U2 - U1) + P (V2 - V1)
= (U2 - U1) + mR (T2 - T1)
mcv (T2 - T1) = U2 - U1 therefore
mcp (T2 - T1) = mcv (T2 - T1) + mR (T2 - T1) therefore
cp = cv + R... and ..
cp - cv = R = PV/mT
|