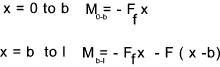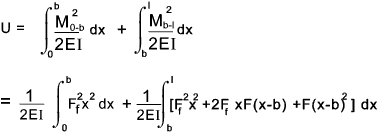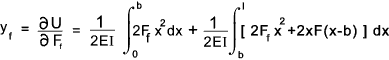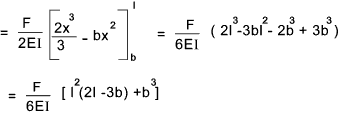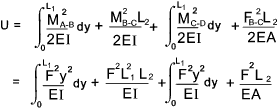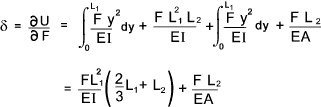When external forces are applied to an beam or structure the structure distorts.  The external forces perform work and the energy is stored in the structure in the form stress and elastic deformation.  In conformance with the law of conservation of energy the work done in the small movements of the external forces (W) must be equal to the potential energy U stored in the structure.

External Work Done = Internal Energy Stored

W = U

When the external forces are removed the beam or structure rebounds elastically, and the stored potential energy returns to zero.....

This simple concept provides methods of investigating the deflections of beams and structures under external loading.  These methods called energy methods are completely independent of the normal stress/strain methods described elsewhere and are often much more convenient to apply.   Castigliano theorem is the best known energy method and notes on the application of this thoerem are provided on this webpage

The notes below provide a very basic introduction to the theorem.  For detailed notes reference to specialist literature is required..

This method provides a means of finding a particular deformation at a particular point.   Unlike the method of double integration, it does not provide general equations for linear and angular deformations for every point on a beam or structure.  For may problems a particular solution is often the only information required and the energy method is the most convenient option

Castiglianos's theorem is stated below

When forces act on elastic systems subject to small displacements, the displacement corresponding to any force collinear with the force is equal of the partial derivative to the total strain energy with respect to that force.
The sign of the displacement is positive, if the displacement is in the same direction as the force

Mathematically Catigliano's theorem is stated as follows..

δ _i is the displacement of the point of application of the force F _i in the direction of F _i..

For angular displacement (rotational) This equation can be expressed as follows

θ _i is the rotational displacement (radians) of the moment M _i in the direction of M _i ..

This method is very useful for obtaining the displacement of a point where there is no force or moment.   In this case a force/ moment is created and then made zero at a suitable point in the analysis.

The procedure to be applied in using Castiglianos's theorem is as follows

a) To determine a deflection y _i in the direction of a real or fictitious force F _f

a) To determine an angular deflection θ _f in the direction of a real or fictitious moment M _f

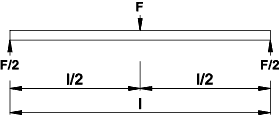
Consider a simply supported beam with a central load F.   The deflection at the central load point is to be determined.
l= 2m,    b=0,1m,    h= 0,05m,    F=10 000N,  E = 206 GPa,   G = 78,610,    I = 4,17.10^-6m⁴

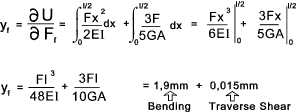
For this example it is assumed that the beam is a rectangle width b and depth h.   The strain energy for bending and for traverse shear is included in the consideration.   Because the beam is symmetrical the deflection at the central point is obtained by doubling the solution from 0 to l/2.
x = the distance from the left hand support.

Moment M = (F/2).x and Tranverse Force V = F/2

With reference to the webpage on strain energy    Strain Energy

1) The expression for the total strain energy =

2) From Castigiano's theorem the deflection of the Force F in the direction of F    y _f = ∂U /∂ F _f

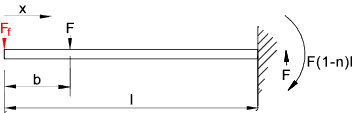
As can be seen from the above example the deflection resulting from the traverse shear is about 0,8% that of resulting from bending and is therefore generally ignored...

Consider the cantilever beam with a load F at a distance b from the free end.   The deflection at the free end is required and so a fictitious load F_f has been added.   The strain energy due to traverse shear loading can be neglected.

The expression for the moment is

1) With reference to the webpage on strain energy    Strain Energy The equation for the strain energy is therefore..

2) From Castigiano's theorem the deflection of the Force F_f in the direction of F_f    y _f = ∂U /∂ F _f

3) Setting F_f to zero and integrating for x results in

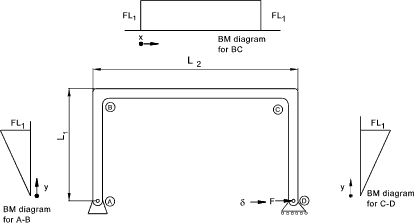
Consider the frame as shown below with one leg free to move horizontally and the other leg pivotted.   A horizontal force F is applied to the free leg and the deflection of the free leg is required.  The strain energy due to traverse shear loading can be neglected.

The expression for the moment in CD M = Fy
The expression for the moment in BC M = FL₁
The expression for the moment in AB M = Fy
The expression for the Tensile force in BC = F

1) With reference to the webpage on strain energy    Strain Energy The equation for the strain energy is therefore..

2) From Castigiano's theorem the deflection of the Force F in the direction of F    δ = ∂U /∂ F _f