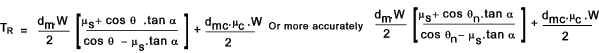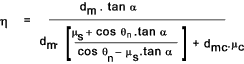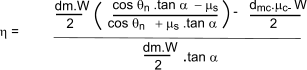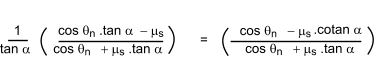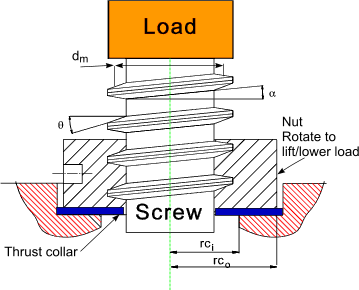
This page includes notes, figures and equations relevant to calculating the torque required to operate powers screws when used as lifting or moving machines.

θ = Thread angle ...(radians)
η = Screw Efficiency
d_m = Mean screw dia...(m)
d_mc = Mean collar dia...(m)
μ_c = coefficient of friction of the screw /thrust collar surfaces
μ_s = coefficient of friction of the screw surfaces
F = Force to rotate thread (Torque /Mean Radius)-(N)
l = lead of thread = n.p...(m)
n = number of threads.
p = pitch between adjacent threads... (m)
α = Helix /lead angle (radians) = tan^-1 l/(π.d_m ).
rc_i = Collar inside radius (m)
rc_o = Collar outside radius (m)
r_m = Mean radius of thread (m)
W = Vertical force generated by screw-(N)
r_mc = Thrust collar mean radius = ( r_ci + r_co ) /  2 ...(m)
T_R = Torque to raise load ...(Nm)
T_L = Torque to lower load ...(Nm)
T_o = Overhaul torque resulting from load ...(Nm)

Note: These notes have been based on W being a vertical force i.e a wieght is being lifted or lowered . As an example a 1000kg mass would result in a vertical load of 1000.g = 9810 N.   . The equations are equally valid if the Force (W) is simply an axial force along the screw axis

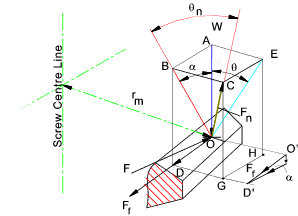
Consider a Force F applied at a mean radius r_m which causes the load to be raised. The nut is turning the screw is prevented from turning.

The sketch above identifies the reactive forces acting at point O on the screw thread surface.
The reactive force F_n acting normal to the surface has the following components in the plane of interest ABDO.

The sketch below illustrates the horizontal and vertical forces acting at a representative point at a radius r _m in the plane normal to the radius.
For equilibrium the sum of all vertical forces = 0 and the sum of all horizontal forces = 0

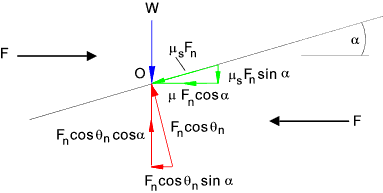
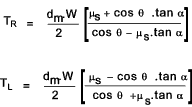
Summing the forces in the vertical direction results in.

F_n cos θ_ncos α = W + F_f sin α

The coefficient of friction for the screw surface materials is μ_s   : F_f = μ_s.F_n and therefore.

F_n = W / ( cosθ_ncos α - μ_s.sin α )..........Equation A

Summing the moment of the forces around the centerline of the screw to obtain T_R , the torque to raise the load W up the incline of the screw.

T _R   =   F.r _m   =   r _m.(F _f cos α + F _n cos θ_nsin α )    =  r _m.(μ_s.F _n. cos α + F _n cos θ_nsin α )

There is an additional friction torque resulting from the friction force on the thrust collar see top sketch above.  This friction force = μ_c. W. ( μ_c = coefficient of friction between the screw thrust surface and the collar surface.).  This friction torque is assumed to be acting at the thrust collar mean radius r_mc

The total torque required to raise the load W is therefore equal to

T _R   =  r _m.(μ _s.F _n cos α + F _n cos θ_nsin α ) + r_mc.μ_c. W

Substituting for F_n.. see equation A above and replacing r_m by d_m/2 ..( and r_mc by d_mc /2 )

dividing the first term numerator and denominator by cos α results in..

.........Equation B

T_r = the torque in Nm to lift the load W (N)//

BC = AE = OA tan θ = (OB cosα). tanθ ..therefore
tan θ_n = BC/OB = cos α. tan θ ..therefore
θ_n = tan^-1 [ cos α. tan θ]

For many applications the helix angle is small compared to the thread angle and therefore cos α is approximately equal to 1. e.g. For M20 2.5 pitch the value of cos α = 0.999


Therefore it is reasonable to let tan θ_n = tan θ and therefore θ_n = θ. ..
[However for multi start screws or screws with a relatively course lead (pitch) it is necessary to use θ_n ]

For normal screws and fine pitch power screws the above equation for T_R can be written as :

The torque to lower the load is written as follows

These equations can be expressed in terms of the lead by substituting the relationship tan α = l / (θ.d_m )

For applications where the thrust is taken on ball or roller thrust bearing the value of μ_c is sufficiently low that it can be taken as approximately 0 and therefore the second term can be ignored.    The approximate equations reduce to..

Overhauling occurs when the screw helix angle is such that the load W would cause to screw to rotate when the rotating force F = zero i.e. the Force is not only required to raise the load - it is also required to statically support the load .

The overhauling torque T_o as calculated below will cause the screw to overhaul when T_o is less than zero.

If the thrust collar torque is assumed to be near zero then the helix angle which allows overhauling (T_o = < zero) can be solved.

tan α = < μ_s / cos θ_n

The efficiency of a screw thread (Forward-Raising)can be defined as follows

η = Torque to raise load (zero friction) / Torque to raise load

Using equation B above the value of T_R resulting when μ_s = 0 =

Dividing this by equation B to provides an equation for the efficiency of the power screw thread.

If the collar friction is very low compared to the screw friction the equation reduces to

Values of μ_s and μ_c are found on the friction coefficients page of this website Power screw friction factors

The efficiency of a screw thread (Backdriving -Lowering)can be defined as follows

η = Back torque generated /Back Torque generated (zero friction)

Using equation C above the value of T_R resulting when μ_s = 0 =

Dividing equation C by this equation provides an equation for the efficiency of the power screw thread.

If the collar friction is very low compared to the screw friction the equation reduces to

Values of μ_s and μ_c are found on the friction coefficients page of this website Power screw friction factors