Helical gears are similar to spur gears except that the gears teeth are at an angle with the axis of the gears.  A helical gear is termed right handed or left handed as determined by the direction the teeth slope away from the viewer looking at the top gear surface along the axis of the gear.   ( Alternatively if a gear rests on its face the hand is in the direction of the slope of the teeth) .   Meshing helical gears must be of opposite hand. Meshed helical gears can be at an angle to each other (up to 90^o ).  The helical gear provides a smoother mesh and can be operated at greater speeds than a straight spur gear.   In operatation helical gears generate axial shaft forces in addition to the radial shaft force generated by normal spur gears.


In operation the initial tooth contact of a helical gear is a point which develops into a full line contact as the gear rotates.   This is a smoother cycle than a spur which has an initial line contact.  Spur gears are generally not run at peripheral speed of more than 10m/s. Helical gears can be run at speed exceeding 50m/s when accurately machined and balanced.

A helical gear train with parallel axes is very similar to a spur gear with the same tooth profile and proportions.  The primary difference is that the teeth are machined at an angle to the gear axis.

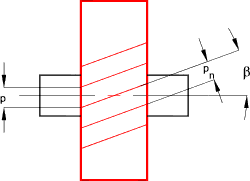
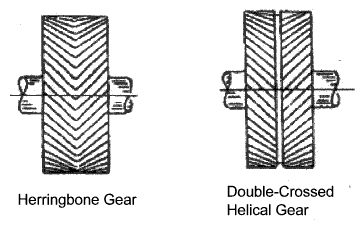
The helix angle of helical gears β is generally selected from the range 6,8,10,12,15,20 degrees. The larger the angle the smoother the motion and the higher speed possible however the thrust loadings on the supporting bearings also increases.   In case of a double or herringbone gear β values 25,30,35,40 degrees can also be used.  These large angles can be used because the side thrusts on the two sets of teeth cancel each other allowing larger angles with no penalty

For helical gears the circular pitch is measured in two ways
The traverse circular pitch (p) is the same as for spur gears and is measured along the pitch circle
The normal circular pitch p _n is measured normal to the helix of the gear.
The diametric pitch is the same as for spur gears     ... P = z _g /d_g = z _p /d _p ....d= pitch circle dia (inches).
The module is the same as for spur gears     ... m = d_g/z _g = d _p/z _p.... d = pitch circle dia (mm).

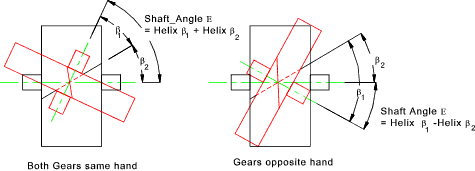
When two helical gears are used to transmit power between non parallel, non-intersecting shafts, they are generally called crossed helical gears.  These are simply normal helical gears with non-parallel shafts.  For crossed helical gears to operate successfully they must have the same pressure angle and the same normal pitch.   They need not have the same helix angle and they do not need to be opposite hand.   The contact is not a good line contact as for parallel helical gears and is often little more than a point contact.  Running in crossed helical gears tend to marginally improve the area of contact.

The relationship between the shaft angles E and the helix angles β ₁ & β₂ is as follows

E = (Same Helix Angle) β ₁ + β ₂ ......(Opposite Helix Angle) β ₁ - β ₂

a = m * [(z ₁ / cos β ₁) + ( z ₁ / cos β ₁ )] / 2

The sliding velocity V_sof crossed helical gears is given by

V_s = (V₁ / cos β ₁ ) = (V ₂ / cos β ₂ )

Designing helical gears is normally done in accordance with standards the two most popular series are listed under standards above: The notes below relate to approximate methods for estimating gear strengths. The methods are really only useful for first approximations and/or selection of stock gears (ref links below). � Detailed design of spur and helical gears should best be completed using :

a) Standards.
b) Books are available providing the necessary guidance.
c) Software is also available making the process very easy.    A very reasonably priced and easy to use package is included in the links below (Mitcalc.com)

The determination of the capacity of gears to transfer the required torque for the desired operating life is completed by determining the strength of the gear teeth in bending and also the durability i.e of the teeth ( resistance to wearing/bearing/scuffing loads ) .. The equations below are based on methods used by Buckingham..

The Lewis formula for spur gears can be applied to helical gears with minor adjustments to provide an initial conservative estimate of gear strength in bending.    This equation should only be used for first estimates. 

σ = F_b / ( b_a. m. Y )

When a gear wheel is rotating the gear teeth come into contact with some degree of impact.  To allow for this a velocity factor is introduced into the equation.   This is given by the Barth equation for milled profile gears.

K _v = (6,1 + V ) / 6,1

V = the pitch line velocity = PCD.w/2

The Lewis formula is thus modified as follows

σ = K _v.F_b / b_a. m. Y

The Lewis form factor Y must be determined for the virtual number of teeth z' = z /cos³β The bending stress resulting should be less than the allowable bending stress S_b for the gear material under consideration.   Some sample values are provide on this page ef Gear Strength Values

The allowable gear force from surface durability considerations is determined approximately using the simple equation as follows

F_w = K _v d _p b _a Q K / cos²β

Q = 2. d_g /( d_p + d_p ) = 2.z_g /( z_p +z_p )

F_w = The allowable gear load. (MPa)

K = Gear Wear Load Factor (MPa) obtained by look up ref Gear Strength Values