Thick Cylinder basics
Consider a thick cylinder subject to internal pressure p 1 and an external pressure p2.
Under the action of radial pressures on the surfaces the three principal
stress will be σ r compressive radial stress, σ t tensile
tangential stress and σ a axial stress
which is generally also tensile. The stress conditions occur throughout the section
and vary primarily relative to the radius r.
It is assumed that the axial stress σ a is
constant along the length of the section...This condition generally applies
away from the ends of the cylinder and away from discontinuities.
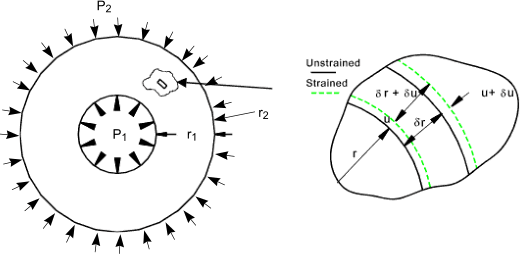
Consider a microscopically small area under stress as shown. u is the radial displacement
at radius r . The circumferential (Hoop) strain due to the internal pressure is
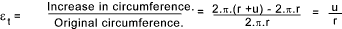
At the outer radius of the small section area (r + δr ) the radius
will increase to (u + δ ). The
resulting radial strain as δr -> 0 is
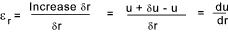
Referring to the stress/strain relationships as stated above. The following
equations are derived.
Basis of equations...
σ r is equivalent to σ 1...
σ t is equivalent to σ 2...
σ a is equivalent to σ 3...
derived equations
Eq. 1)......E ε a = σ a - υσ t - υσ r
Eq. 2)......E.ε t = E.u/r = σ t - υσ a - υσ r
Eq. 3)......E.εr = E.du/dr = σ r - υσ t - υσ a
Multiplying 2) x r
Eu = r ( σ t - υσ a - υσ r )
differentiating
Edu/dr = σ t - υσ a - υσ r +
r. [ dσ t /dr - υ.( dσ a / dr ) - υ.( dσ r / dr ) ]
= σ r - υσ t - υσ a ..( from 3 above )
Simplifying by collecting terms.
Eq. 4)........(σ t - σ r ). ( 1 + υ ) + r.(dσ t/ dr ) - υ.r.(dσ a / dr ) - υ.r.(dσ r / dr) = 0
Now from 1) above since ε a is constant
dσ a / dr = υ.(dσ t / dr + dσ r / dr )
Substituting this into equation 4)
( σ t - σ r )( 1 + υ ) + r ( 1 - υ 2 ).( dσ t/dr ) - υ.r.( 1 + υ )( dσ r / dr ) = 0
This reduces to..
Eq. 5).....σ t - σ r + r( 1 - υ ).(dσ t / dr ) - υ.r.(dσ r / dr ) = 0
Now considering the radial equilibrium of the element of the section. Forces based on unit length of cylinder
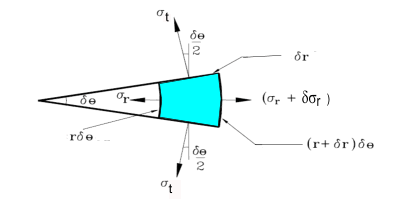
(σ r + δ σ r )(r + δ r)δθ
- σ r r δ θ - 2σ t δ r.sin [(1/2) δ θ ] = 0
In the limit .sin [(1/2) δ θ ] - > [(1/2) δ θ ]
and neglecting small products the equation reduces to..
σr δ r + δσr.r
-σ t δ r = 0... and as δ r --> 0 then σr. d r + dσr.r
-σ td r = 0...as δ and this results in..
Eq.6)....σr + r. (d σr/dr ) = σ t
Now eliminating σ t by substituting eq 6 into eq 5)
σr + r. (d σr/dr ) - σ r
+ r( 1 - υ ).(dσ t / dr ) - υ.r.(dσ r / dr ) = 0
r( 1 - υ )(d σr/dr )
+ r( 1 - υ ).(dσ t / dr ) = 0
simpifying to
(d σr/dr )
+ (dσ t / dr ) = 0
Integration of this equation results in
Eq.7)....
σr + σ t = 2.A (constant of integration.)
substituting this into equation 6 to eliminateσt
σr + r. (d σr/dr ) = 2.A - σr
Therefore
2.A = 2. σr + r. (d σr/dr )
which is equivalent to 2.A = (1 /r ). d ([ r2. σ r ]/dr )
therefore 2.A.r = (d[r2.σr]/dr )
Which on integrating gives σr.r2 = A..r2 + B
with resulting
Eq 8) σr = A + B / r 2 and substituting this into Eq. 7)
Eq 9) σt = A - B / r 2
General Equation for Thick Walled Cylinder
The general equation for a thick walled cylinder subject to internal and external
pressure can be easily obtained from eq)8 and eq) 9 as follows.
Consider a cylinder with and internal diameter d 1, subject to an
internal pressure p 1. The external diameter is d 2 which
is subject to an external pressure p 2.
The radial pressures at the surfaces are the same as the applied pressures therefore
σ r = A + B / r 2
σ t = A - B / r 2
The radial pressures at the surfaces are the same as the applied pressures therefore
- p1 = A + B / r 12
-p2 = A + B / r 22
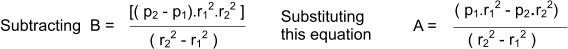
The resulting general equations are known as Lame's Equations and are shown as follows