Mechanics Index

Rotating Disks and Cylinders

Introduction..... Symbols..... Assumptions..... Basic Equations for a Rotating Disk..... Basic Equations for a Rotating Cylinder.....

Introduction

These notes relate to the stresses and strains existing in thick walled cylinders when rotated at speed they are generally applicable to design of flywheels.   The primary assumption is that the cylinders are not subject to internal or external prssure.    A basic review of solid disks, rings and cylinders is carried out.

Members of excelcalcs.com can upload a spreadsheet including all of the derived equations below at ExcelCalcs.com calculation Stresses in Rotating Disks & Rings ...


Symbols / Units

Tensile stresses are considered positive and compressive stresses are negative.

p 1 = Internal pressure (N/m2)
p 2 = External pressure (N/m2)
σ r = radial (N/m2)
σ t = tangential stress (N/m2)
σ a = axial/longitudonal stress (N/m2)
E = Young's moudulus of elasticity (N/m2)
ρ = density. ( kg/m2)
υ = Poisson's ratio
r = radius at point or analysis (m).
R 1= inside radius of cylinder (m).
R 2= outside radius of cylinder (m).
εr = radial strain
εt = tangential strain
εa = axial /longitudinal strain
u = radial deflection (m)


Initial Assumptions

The following relationships are assumed for the strains ε1,ε2, ε3 associated with the stress σ 1, σ 2 and σ 3.
υ = Poisson's ratio.

Reference Notes on stress and strain

ε1 = σ 1 /E   -   υσ 2 /E    -    υσ 3 /E
ε2 = σ 2 /E   -   υσ 1 /E    -    υσ 3 /E
ε3 = σ 3 /E   -   υσ 1 /E    -    υσ 2 /E


Thick Disk basics

Consider a "disk"/ "thin ring" subject internal stresses resulting from the inertial forces as a result of its rotational speed.    Under the action of the inertial forces only, the three principal stress will be σ  r tensile radial stress, σ t tensile tangential stress and σ a and axial stress which is generally also tensile.  The stress conditions occur throughout the section and vary primarily relative to the radius r.    It is assumed that the axial stress σ a is constant along the length of the section and because the disk is thin compared to its diameter the axial stress throughout the section is assumed to be zero.It is also assumed that the internal pressure (P1 ) and the external pressure ( P2 ) = 0.

Consider a microscopically small area under stress as shown.   u is the radial displacement at radius r .  The circumferential (Hoop) strain due to the internal pressure is

At the outer radius of the small section area (r + δr )   the radius will increase to (u + δ ).   The resulting radial strain as δr -> 0 is

Referring to the stress/strain relationships as stated above.   The following equations are derived.   

Basis of equations...
σ r is equivalent to σ 1...
σ t is equivalent to σ 2...
σ a is equivalent to σ 3...

derived equations

Strictly the following equations apply
Eq. 1)......E ε a = σ a - υσ t - υσ r
Eq. 2)......E.ε t = E.u/r = σ t - υσ a - υσ r
Eq. 3)......E.εr = E.du/dr = σ r - υσ t - υσ a
However because of the assumption that σ a = 0 the equations are modified as follow.

Eq. 1)......E ε a =0 - υσ t - υσ r
Eq. 2)......E.ε t = E.u/r = σ t - υσ r
Eq. 3)......E.εr = E.du/dr = σ r - υσ t -

Multiplying 2) x r

Eu = r ( σ t -- υσ r )

Differentiating

Edu/dr = σ t - υσ r + r. [ dσ t /dr - υ.( dσ r / dr ) ] = σ r - υσ t .. from 3 above )

Simplifying by collecting terms.

Eq. 4)........(σ t - σ r ). ( 1 + υ ) + r.(dσ t/ dr ) ) - υ.r.(dσ r / dr) = 0

Now considering the radial equilibrium of the element of the section. Forces based on unit length of cylinder

2.σ t. δ r.sin(1/2.δθ) + σrδθ - (σ r + δσ r) (r + σ r )θδθ = ρr2 ω2δr δθ


In the limit this reduces to


Eq 5 )..... σ t - σ r - r dσ r / d r = ρr2 ω2


Substitute for σ t - σ r in Equation 4 results in


( r dσ r / d r + ρr2 ω2 ). ( 1 + υ ) + r.(dσ t/ dr ) ) - υ.r.(dσ r / dr) = 0

Therefore


dσ t/dr + dσ r/dr = - ρrω 2(1+υ)

Integrating


Eq 6 )..... σ t + σ r = - ρ r2 ω 2(1+υ)/2 + 2A

Subtract equation 5...


2.σ r + r.dσ r/dr = - ρr2ω 2(3+υ)/2 + 2A

This is the same as


(1/r).d (σ r.r2)dr = - ρ r2 ω 2(3+υ)/2 + 2A

Integrating


σ r.r2 = - (ρ r4 ω 2(3+υ)/8 + Ar2 + B

Eq 7 ...

σ r = A + B/r2 - (3 + υ)ρ r2 ω 2/8

Eq 8 ......combining Eqn. 7 with Eqn. 6

σ t = A - B/r2 - ( 1+ 3υ)ρ r2 ω 2/8

1) Solid Disk

At the centre the B/r2 term implies infinite stresses which are clearly not credible and therefore B must equal 0.     At r = R2 on the outside edge of the disk. the radial stress is equal to the surface stress which is equal to 0. Therefore at R2

σ r= 0 = A - (3 + υ)ρ R2 2 ω 2/8

Therefore A = ρ R2 2 ω 2/8
B = 0

σ t = (ρ ω 2/8)[ (3 + υ)R2 2 - (1 + 3υ) r2]

σ r = (ρ ω 2/8)[ (3 + υ)( R2 2 - r2)]

The maximum stress is at the centre

σ t_max = σ r_max = (ρ ω 2/8).(3 + υ)R2 2

2) Disk with a hole

At the outside edge r = R2 and at the hole radius r = R1 the radial surface stress is asssumed to be 0

Therefore
σ r= 0 = A + B/R22 - (3 + υ)ρ R22 ω 2/8
σ r= 0 = A + B/R12 - (3 + υ)ρ R12 ω 2/8

Solving
B = -(3 + υ)ρ ω 2/8.(R12 . R22)

A = (3 + υ)ρ ω 2/8.(R12 + R22)

σ r = (3 + υ)ρ ω 2/8) (R12 + R22 - R12.R22/ r2 - r2 )

σ t = ρ ω 2/8) [(3 + υ)(R12 + R22 + R12.R22/ r2) - (1+3υ) r2 )]
The maximum tangential stress σ t is at the inside hole surface and equals
σ t_max = ρ ω 2/4) [ (1- υ)R12 + (3 + υ)R22)]

The maximum radial stress σ r is at r = sqrt (R 1. R2 ) and equals .
σ r_max = (3+υ) (ρ ω 2/8)(R2 - R1)2

2) Cylinders

The primary difference between a long rotating cylinder and a thin one is that it the axial stress σ a is not equal to 0.    The assumption in this case is that the longitudonal strain ε a is constant: cross sections remain plane.

Basis of equations... Refer to introductory notes at the top of webpage
σ r is equivalent to σ 1...
σ t is equivalent to σ 2...
σ a is equivalent to σ 3...

derived equations

Eq. 1)......E ε a = σ a - υσ t - υσ r
Eq. 2)......E.ε t = E.u/r = σ t - υσ a - υσ r
Eq. 3)......E.εr = E.du/dr = σ r - υσ t - υσ a

Multiplying 2) x r

Eu = r ( σ t - υσ a - υσ r )

differentiating

Edu/dr = σ t - υσ a - υσ r + r. [ dσ t /dr - υ.( dσ a / dr ) - υ.( dσ r / dr ) ] = σ r - υσ t - υσ a ..( from 3 above )

Simplifying by collecting terms.

Eq. 4)........(σ t - σ r ). ( 1 + υ ) + r.(dσ t/ dr ) - υ.r.(dσ a / dr ) - υ.r.(dσ r / dr) = 0

Now from 1) above since ε a is constant then dσ a /dr = υ (dσ t/dr + dσ r /dr )

substituting for dσ a/dr in Eq 4)

(σ t - σ r ). ( 1 + υ ) + r.(dσ t/ dr ) - υ.r.(υ (dσ t/dr + dσ r /dr ) - υ.r.(dσ r / dr) = 0

(σ t - σ r ). ( 1 + υ ) + r.(1-υ2)(dσ t/ dr ) - υ.r.(1 + υ ) (dσ r/dr) = 0

(σ t - σ r ) + r.(1-υ)(dσ t/ dr ) - υ.r (dσ r/dr) = 0

Now considering the radial equilibrium of the element of the section as shown in the notes above Eq. 5 results

Eq 5........ σ t - σ r - r dσ r / d r = ρr2 ω2

Substitute for (σ t - σ r )

r.(1-υ)(dσ t/ dr )     +    (1 - υ).r (dσ r/dr) = - ρr2 ω2

Therefore

(dσ t/ dr ) + (dσ r/dr) = - ρ r ω2 /(1-υ)

Integrating

Eq.6)... σt + σr = -ρr2ω2 /2(1-υ) + 2A

This is similar to the equation 6 for the Rotating Disk analysis completed above. In fact the rotating disks equation can apply for the long cylinder if (1 + υ ) in the disk equations are replace by 1 / (1 - υ ) . Or if υ is replaced by (υ / (1- υ)..


Now eliminating σ t by substituting into Eq 5)
2σ r + r dσ r / d r = 2A - ρr2ω2 - ρr2ω2 /2(1-υ)

Therefore

(1/r).d(σr.r2)/dr = 2A - ρr2ω2(3- 2υ ) /2(1-υ)

Therefore

d(σr.r2)/dr = 2Ar - ρr3ω2(3- 2υ ) /2(1-υ)

Integrating

Eq.7).... σr = - ρr2ω2(3- 2υ ) /8(1-υ) + A - B / r2

Now substituting for σr in Equation 7 to obtain σt

Eq.8).... σt = - ρr2ω2(1 + 2υ ) /8(1-υ) + A + B / r2

Solving for A and B for a solid cylinder

At the centre of the cylinder R1 = 0 the stresses cannot be infinite so B is cleraly equal to 0.

B = 0

At the outside diameter of the cylinder r = R2 .

σ r = 0 = σr = - ρr2ω2(3- 2υ ) /8(1-υ) + A

Therefore

A = ρω2R22(3- 2υ ) /8(1-υ)

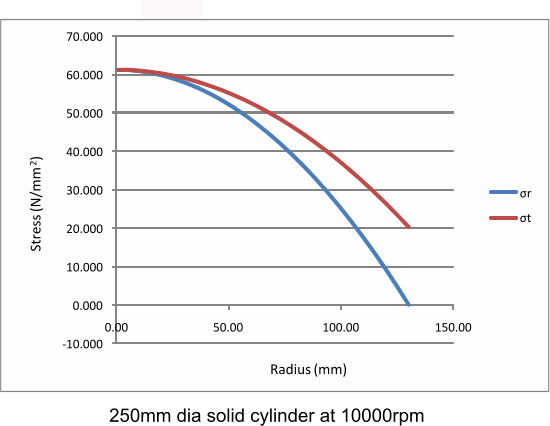
Eq.9).... .σr = ρω2(3- 2υ ) /8(1-υ ) (R2 2 - r 2)

Eq.10).... σt = ρω2 /8(1-υ) [(3- 2υ )R22 - (1 + 2υ ) r2 ]

The maximum radial stress and tangential stress are equal at r = 0 =

σr_max = σt_max = ρω2(3- 2υ ) /8(1-υ ))R22

Solving for A and B for a hollow cylinder

At r = R1 and at r = R2 the radial stress σr = 0

Therefore 0 = σr = - ρ R12ω2(3- 2υ ) /8(1-υ) + A - B / R12

Therefore 0 = σr = - ρ R22ω2(3- 2υ ) /8(1-υ) + A - B / R22

Therefore ... ρ R12ω2(3- 2υ ) /8(1-υ) + B / R12 = ρ R22ω2(3- 2υ ) /8(1-υ) + B / R22

ρ (R12 - R22)ω2(3- 2υ ) /8(1-υ) = ρ B / R22 - B / R12

Therefore B = R12.R22.ρ ω2(3- 2υ ) /8(1-υ)

Solving for A

0 = σr = - ρR12ω2(3- 2υ ) /8(1-υ) + A - R22.ρ ω2(3- 2υ ) /8(1-υ)

Therefore A = (R22 + R12).ρ ω2(3- 2υ ) /8(1-υ)

Resulting in..



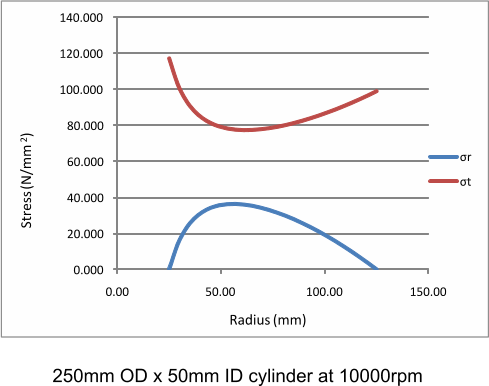
σr = ρω2(3- 2υ ) /8(1-υ ) [ - r2 + (R22 + R12) - (R12.R22)/r2 ]

σr_max = ρω2(3- 2υ ) /8(1-υ ) ((R22 - R12)... Is located at at r = Sqrt (R1.R2 )

σt = ρω2 /8(1-υ ) [ - r2 (1 + 2υ ) + (3- 2υ ) {( R22 + R12) + (R12.R22)/r2} ]

σt_max = ρω2 /4(1-υ ) [ (1 - 2υ )R12 + (3- 2υ )R22] ... Is located at r = R1.



Relevant Links
  1. Rotating Disks and Cylinders Similar Notes to mine using different (american?) terminology.
  2. Dan Notes Thick Walled Cylinders Excellent source of information on this topic


Mechanics Index

Remember - the information on this site is for general information purposes only and while we endeavour to keep the information up to date and correct, we make no representations or warranties of any kind, express or implied, about its completeness, accuracy, reliability, suitability or availability. Any reliance you place on such information is therefore strictly at your own risk.

Roy Beardmore passed away on 9th March 2013. He is sadly missed. This website, Roymech, has been an invaluable resource for engineers around the world and we hope to maintain this incredible legacy going forward.

Have a question? Contact us.

© 2020 Roymech.org