Introduction
When a component is subject to increasing loads it eventually fails. It is comparatively
easy to determine the point of failure of a component subject to a single tensile force. The strength
data on the material identifies this strength. However when the material is subject to a number of loads
in different directions some of which are tensile and some of which are shear, then the determination
of the point of failure is more complicated...
Metals can be broadly separated into DUCTILE metals and BRITTLE metals. Examples of ductile metals include
mild steel, copper etc . Cast iron is a typical brittle metal.
Ductile metals under high stress levels initially deform plastically at a definite yield point
or progressively yield. In the latter case a artificial value of yielding past the elastic
limit is selected in lieu of the yield point e.g 2%proof stress. At failure a ductile metal
will have experienced a significant degree of elongation.
Brittle metals experience little ultimate elongation prior to failure and failure is generally
sudden.
A ductile metal is considered to have failed when it has suffered elastic failure, that is when
a marked plastic deformation has begun. A number of theories of elastic failure
are recognised including the following:
- Maximum principal stress theory ..... Can be used - with caution for brittle metals
- Maximum shear stress theory
- Distortion energy theory.....Favoured for ductile metals
- Constant distortion energy theory
|
The maximum principal stress theory ..The theory associated with Rankine.
This theory is approximately correct for cast iron and brittle materials generally.
According to this theory failure will occur when the maximum principal stress in a system
reaches the value of the maximum strength at elastic limit in simple tension. For the two
dimensional stress case this is obtained from the formula below (ref page on Mohrs circle).
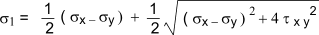
The design Factor of Safety for the two dimensional case=
FoS = Elastic Limit from tensile test / highest principal stress.
The Maximum Shear Stress Theory ..
The theory associated with Tresca and Guest.
This is very relevant to ductile metals. It is conservative and relatively easy to
apply. It assumes that failure occurs when a maximum shear stress attains a
certain value. This value being the value of shear strength at failure in
the tensile test. In this instance it is appropriate to choose the yield point
as practical failure. If the yield point = Sy and this is obtained from a tensile
test and thus is the sole principal stress then the maximum shear stress Ssy
is easily identified as Sy /2 . (ref to notes on Mohrs circle).. Mohr's Circle
Ssy = Sy /2
In the context of a complicated stress system the initial step would be to determine the principle
stress i.e. σ1, σ1 &
σ3-
in order of magnitude
σ1 > σ2
> σ3..
then the maximum shear stress
would be determined from
Maximum Shear Stress = τ max
= Greatest of
( σ1 - σ2 ) / 2 :
( σ2 - σ3 ) / 2 :
( σ1 - σ3 ) / 2 =
( σ1 - σ3 ) / 2
The factor of safety selected would be
FoS = Sy / ( 2 . τ max )
= Sy / ( σ1 - σ3 )
The theory is conservative especially if the yield strength is more then 50% of the tensile strength..
For the simple case of a tensile stress σx combined with a shear stress τ xy . The design FOS +
FoS = Sy / ( σx 2 + 4. τ xy 2 )1/2
For a case of a component with σ 1 >
σ2 both positive (tensile) and with
σ3 = 0
then the maximum shear stress = ( σx - 0 ) / 2
Distortion Energy Theory
Also called Shear Strain Energy Theoty This theory is also known as the Von Mises-Hencky theory
Detailed studies have indicated that yielding is related to the shear energy rather than the maximum
shear stress..
Strain energy is energy stored in the material due to elastic deformation.
The energy of strain is similar to the energy stored in a spring.
Upon close examination, the strain energy is seen to be of two kinds : one part
results from changes in mutually perpendicular dimensions , and hence in volume,
with no change angular changes: the other arises from angular distortion without
volume change. The latter is termed as the shear strain energy , which has been
shown to be a primary cause of elastic failure..
It can be shown by strain energy analysis that the shear strain energy associated
with the principal stresses σ1,
σ1 &
σ3
at elastic failure, is the same as than in the tensile test causing yield
at direct stress Sy when:
(σ1 - σ2) 2 +
(σ2 - σ3) 2 +
(σ1 - σ3 ) 2 > =
2 Sy2
In terms of 3 dimensional stresses using Cartesian co-ordinates
( σx - σy) 2 +
( σy - σz) 2 +
( σz - σx ) 2 +
6. ( τ xy2 + τ yz2 + τ zx2 )
>= 2 Sy2
In terms of plane stress this reduces to..
(σx2 - σx . σy
+ σy2 + 3 .τ xy2 )
>= Sy2
In terms of simple linear stress combined with shear stress..
Factor of Safety FOS = Sy /
( σx2 +
3 .τ xy2 ) 1/2
Strain Energy Theory ..The theory associated with Haigh.
This theory is based on the assumption that strains are recoverable up to the elastic
limit, and the energy absorbed by the material at failure up to this point is a
single valued function independent of the stress system causing it.
The strain energy per unit volume causing failure is equal to the strain energy at the
elastic limit in simple tension..
The following relationship can be derived from this theory. (Sy is the yield point
in simple shear and ν = poissons ratio. )
Failure Occurs with this theory when....
M(σ1 - σ2) 2 +
(σ2 - σ3) 2 +
(σ1 - σ3 ) 2
+ 2 n. (σ1.σ2 +
σ2.σ3 +
σ1.σ3 )
≥ Sy
|