Introduction
A sample x1 , x2.....is taken from a population
and it is necessary to test the hypothesis that F(x) is the distribution function of the population
from which the sample has been taken. The sample distribution function Fs (x) is
an approximation of F(x) and if it approximates it sufficiently well the hypothesis can be accepted. If
it deviates the hypothesis is rejected.
The Chi-squared test is a tool which allows us to determine
how much the Fs (x) distribution can deviate from F(x) if the hypothesis is true. A distribution
of the deviation is created under the assumption that the hypothesis is true and the number c is determined such that
if the hypothesis is true then a deviation greater than c has a preassigned probability called the significance level.
The χ2 statistic (pronounced ki) is defined as
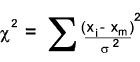
The χ2 distributions is a family of density functions
each one dependent
on the number of freedoms denoted by ν. The exact definition
is too complicated to identify on this level website. This distribution is used
to measure how well theoretical data fits the observed data.
The chi-square distribution has the following properties:
The shapes of the χ2 distributions for various degrees of freedom are shown in the figure below
The mean of the distribution is equal to the number of degrees of freedom: μ = ν.
The variance is equal to two times the number of degrees of freedom: s x 2 = 2 . ν
When the degrees of freedom are greater than or equal to 2, the maximum value for Y occurs when χ2 = ν - 2.
As the degrees of freedom increase, the chi-square curve approaches a normal distribution.
When O is and observed sample frequency and E is the expected sample frequency the statistic for χ2 as shown below
is can be used as an approximation for the true χ2 value
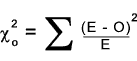
Symbols
n = sample number
χ2 = statistic for testing hypothesis
c = limit of χ2 defining sample significance
f(x) = probability function. (values between 0 and 1)
F(x) = probability distribution function.
ν = number of degrees of freedoms
var = sample variance
K = number of classes /intervals
Jj class designation
Φ (z) = Probability distribution function.(Standardised probability )
|
α = significance value
μ = population /random variable mean
σ 2 = population /random variable variance
σ = population /random variable standard deviation
xm = arithmetic mean of sample
sx 2 = variance of sample
sx = Standard deviation of sample
z = (x - μ ) / σ Equation to standardise prob'y dist'n function/
|
Procedure.
The notes below are a basic procedure of completing a χ 2 test
that F(x) is the distribution function from which a sample x i..x 2..xn is taken.
Step 1) Divide the x axis into K equal intervals J 1, J 2..J K such that each interval contains
at least 5 values of the given sample. A sample value on a boundary is counted as 0,5 to each side of the boundary.
Step 2) Count the number of sample values b j in each interval J j (j = 1 to K)
Using a table of distribution values for F(x) determine the probability pi that the random variable X assumes any
value in the each interval I j
calculate ej = np j
This is the expected number of samples values if the hypothesis is true
Step 3) Compute the deviation
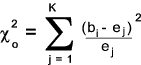
Step 4) Choose a significance value α (0,05, 0,01 , 0,001 etc)
Determine the value of c from
P(χ 2 ≤ c) = 1 - α
using the table of chi_Square distribution with ν degrees of freedom .
[example if 1 - α = 0,95 and ν = 6 deg. of freedom then c = 12,592
If χ o 2 ≤ c
then the hypothesis is accepted . If χ o 2 > c then the hypothesis is rejected.
Note: the procedure described above is illustrated in the examples below
Number of freedom
The number of degrees of freedom ν is taken as
ν =the number of classes /Intervals - 1 = K -1
If any parameters of F(x) (say r parameters) have to be estimated then the number of degrees of freedom =
ν = K - r - 1
Chi Distribution with ν degrees of Freedom.
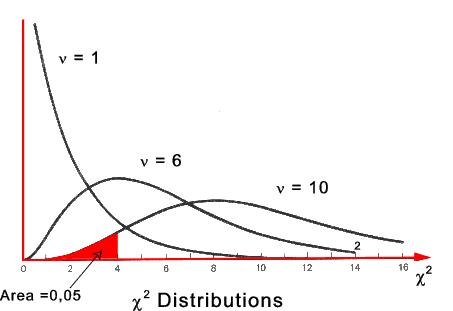
The chi-square distribution shown above are constructed so that the
total area under each curve is equal to 1. The area under the curve between
0 and a particular value of a chi-square statistic is the
cumulative probability associated with that statistic.
For example, in the figure above, the shaded area represents the cumulative
probability for a chi-square equal 3,94 with a (say) a sample size n = 11 with ν
degrees of freedom = (n-1) = 10. The shaded area under the curve = 0,05.
The table below provides Ch-square values relating to F(z) against the number of degrees of freedom
Table of Chi-square values
Degs Of
Freedom
ν |
F(z) |
| 0,005 |
0,01 |
0,025 |
0,05 |
0,95 |
0,975 |
0,99 |
0,995 |
| 1 |
0 |
0 |
0,001 |
0,004 |
3,841 |
5,024 |
6,635 |
7,879 |
| 2 |
0,01 |
0,02 |
0,051 |
0,103 |
5,991 |
7,378 |
9,21 |
10,597 |
| 3 |
0,072 |
0,115 |
0,216 |
0,352 |
7,815 |
9,348 |
11,345 |
12,838 |
| 4 |
0,207 |
0,297 |
0,484 |
0,711 |
9,488 |
11,143 |
13,277 |
14,86 |
| 5 |
0,412 |
0,554 |
0,831 |
1,145 |
11,07 |
12,832 |
15,086 |
16,75 |
| 6 |
0,676 |
0,872 |
1,237 |
1,635 |
12,592 |
14,449 |
16,812 |
18,548 |
| 7 |
0,989 |
1,239 |
1,69 |
2,167 |
14,067 |
16,013 |
18,475 |
20,278 |
| 8 |
1,344 |
1,647 |
2,18 |
2,733 |
15,507 |
17,535 |
20,09 |
21,955 |
| 9 |
1,735 |
2,088 |
2,7 |
3,325 |
16,919 |
19,023 |
21,666 |
23,589 |
| 10 |
2,156 |
2,558 |
3,247 |
3,94 |
18,307 |
20,483 |
23,209 |
25,188 |
| 11 |
2,603 |
3,053 |
3,816 |
4,575 |
19,675 |
21,92 |
24,725 |
26,757 |
| 12 |
3,074 |
3,571 |
4,404 |
5,226 |
21,026 |
23,337 |
26,217 |
28,3 |
| 13 |
3,565 |
4,107 |
5,009 |
5,892 |
22,362 |
24,736 |
27,688 |
29,819 |
| 14 |
4,075 |
4,66 |
5,629 |
6,571 |
23,685 |
26,119 |
29,141 |
31,319 |
| 15 |
4,601 |
5,229 |
6,262 |
7,261 |
24,996 |
27,488 |
30,578 |
32,801 |
| 16 |
5,142 |
5,812 |
6,908 |
7,962 |
26,296 |
28,845 |
32 |
34,267 |
| 17 |
5,697 |
6,408 |
7,564 |
8,672 |
27,587 |
30,191 |
33,409 |
35,718 |
| 18 |
6,265 |
7,015 |
8,231 |
9,39 |
28,869 |
31,526 |
34,805 |
37,156 |
| 19 |
6,844 |
7,633 |
8,907 |
10,117 |
30,144 |
32,852 |
36,191 |
38,582 |
| 20 |
7,434 |
8,26 |
9,591 |
10,851 |
31,41 |
34,17 |
37,566 |
39,997 |
| 21 |
8,034 |
8,897 |
10,283 |
11,591 |
32,671 |
35,479 |
38,932 |
41,401 |
| 22 |
8,643 |
9,542 |
10,982 |
12,338 |
33,924 |
36,781 |
40,289 |
42,796 |
| 23 |
9,26 |
10,196 |
11,689 |
13,091 |
35,172 |
38,076 |
41,638 |
44,181 |
| 24 |
9,886 |
10,856 |
12,401 |
13,848 |
36,415 |
39,364 |
42,98 |
45,558 |
| 25 |
10,52 |
11,524 |
13,12 |
14,611 |
37,652 |
40,646 |
44,314 |
46,928 |
| 26 |
11,16 |
12,198 |
13,844 |
15,379 |
38,885 |
41,923 |
45,642 |
48,29 |
| 27 |
11,808 |
12,878 |
14,573 |
16,151 |
40,113 |
43,195 |
46,963 |
49,645 |
| 28 |
12,461 |
13,565 |
15,308 |
16,928 |
41,337 |
44,461 |
48,278 |
50,994 |
| 29 |
13,121 |
14,256 |
16,047 |
17,708 |
42,557 |
45,722 |
49,588 |
52,335 |
| 30 |
13,787 |
14,953 |
16,791 |
18,493 |
43,773 |
46,979 |
50,892 |
53,672 |
| 31 |
14,458 |
15,655 |
17,539 |
19,281 |
44,985 |
48,232 |
52,191 |
55,002 |
| 32 |
15,134 |
16,362 |
18,291 |
20,072 |
46,194 |
49,48 |
53,486 |
56,328 |
| 33 |
15,815 |
17,073 |
19,047 |
20,867 |
47,4 |
50,725 |
54,775 |
57,648 |
| 34 |
16,501 |
17,789 |
19,806 |
21,664 |
48,602 |
51,966 |
56,061 |
58,964 |
| 35 |
17,192 |
18,509 |
20,569 |
22,465 |
49,802 |
53,203 |
57,342 |
60,275 |
| 36 |
17,887 |
19,233 |
21,336 |
23,269 |
50,998 |
54,437 |
58,619 |
61,581 |
| 37 |
18,586 |
19,96 |
22,106 |
24,075 |
52,192 |
55,668 |
59,893 |
62,883 |
| 38 |
19,289 |
20,691 |
22,878 |
24,884 |
53,384 |
56,895 |
61,162 |
64,181 |
| 39 |
19,996 |
21,426 |
23,654 |
25,695 |
54,572 |
58,12 |
62,428 |
65,475 |
| 40 |
20,707 |
22,164 |
24,433 |
26,509 |
55,758 |
59,342 |
63,691 |
66,766 |
| 41 |
21,421 |
22,906 |
25,215 |
27,326 |
56,942 |
60,561 |
64,95 |
68,053 |
| 42 |
22,138 |
23,65 |
25,999 |
28,144 |
58,124 |
61,777 |
66,206 |
69,336 |
| 43 |
22,86 |
24,398 |
26,785 |
28,965 |
59,304 |
62,99 |
67,459 |
70,616 |
| 44 |
23,584 |
25,148 |
27,575 |
29,787 |
60,481 |
64,201 |
68,71 |
71,892 |
| 45 |
24,311 |
25,901 |
28,366 |
30,612 |
61,656 |
65,41 |
69,957 |
73,166 |
| 46 |
25,041 |
26,657 |
29,16 |
31,439 |
62,83 |
66,616 |
71,201 |
74,437 |
| 47 |
25,775 |
27,416 |
29,956 |
32,268 |
64,001 |
67,821 |
72,443 |
75,704 |
| 48 |
26,511 |
28,177 |
30,754 |
33,098 |
65,171 |
69,023 |
73,683 |
76,969 |
| 49 |
27,249 |
28,941 |
31,555 |
33,93 |
66,339 |
70,222 |
74,919 |
78,231 |
| 50 |
27,991 |
29,707 |
32,357 |
34,764 |
67,505 |
71,42 |
76,154 |
79,49 |
| 60 |
35,534 |
37,485 |
40,482 |
43,188 |
79,082 |
83,298 |
88,379 |
91,952 |
| 70 |
43,275 |
45,442 |
48,758 |
51,739 |
90,531 |
95,023 |
100,425 |
104,215 |
| 80 |
51,172 |
53,54 |
57,153 |
60,391 |
101,879 |
106,629 |
112,329 |
116,321 |
| 90 |
59,196 |
61,754 |
65,647 |
69,126 |
113,145 |
118,136 |
124,116 |
128,299 |
| 100 |
67,328 |
70,065 |
74,222 |
77,929 |
124,342 |
129,561 |
135,807 |
140,17 |
Example 1
A dice is thrown 180 times and the scores are recorded as shown below. Confirm that the dice
is true . A dice is true if there is equal probability of any score 1 to 6.( = 1/6)
| Score | 1 | 2 | 3 | 4 | 5 | 6 |
| Score | 36 | 35 | 25 | 29 | 38 | 24 |
Testing the hypothesis that the dice is true with a 5% level of significance.
There is only one constraint i.e. that the Total number of total of the expected frequencies
∑ E = the total observed frequencies. ∑ O
The number of degrees of freedom ν = 6 - 1 = 5.
With a 1 - α value of 0,95 then c is 11,07 from the table above. If χ 2 < c then hypothesis if accepted
For each toss the expected number of observations =(1/6).180 = 30.
Calculation of the χ 2 is as shown below.
| Observed (O) | Expected (E) | O-E | (O-E)2 | (O-E)2 /E |
| 36 | 30 | 6 | 36 | 1,2 |
| 34 | 30 | 4 | 16 | 0,533 |
| 25 | 30 | 5 | 25 | 0,833 |
| 23 | 30 | 7 | 49 | 1,633 |
| 38 | 30 | 8 | 64 | 2,133 |
| 24 | 30 | 6 | 36 | 1,2 |
| ∑ O = 180 | ∑ E = 180 | | χ 2 =7,533 |
χ 2 =7,533 is less than 11,07 and therefore there is good confidence
that the dice is true.
In this case a continuous distribution is used as a model for testing discrete data. This
is reasonable because there are a significant number of sample values-observations (180)
Example 2
Consider 104 tensile tests on twine resulting in the following table of breaking loads (N).
The sample result to be test to confirm that the population is normal.
The population mean μ and variance σ 2 are not
known.
the
| Breaking load ( Newtons) |
| 201 |
234 |
242 |
250 |
256 |
261 |
267 |
271 |
277 |
282 |
292 |
300 |
310 |
| 203 |
234 |
243 |
250 |
256 |
262 |
267 |
271 |
277 |
283 |
293 |
302 |
312 |
| 221 |
237 |
246 |
252 |
257 |
264 |
268 |
272 |
278 |
284 |
293 |
302 |
315 |
| 224 |
238 |
246 |
252 |
258 |
264 |
268 |
272 |
278 |
286 |
294 |
304 |
316 |
| 224 |
239 |
247 |
252 |
259 |
265 |
268 |
273 |
279 |
287 |
296 |
304 |
321 |
| 229 |
239 |
247 |
253 |
259 |
266 |
269 |
273 |
279 |
289 |
297 |
306 |
326 |
| 231 |
241 |
249 |
254 |
260 |
266 |
270 |
276 |
281 |
291 |
298 |
307 |
341 |
| 231 |
241 |
249 |
256 |
261 |
266 |
271 |
276 |
282 |
291 |
299 |
309 |
342 |
The average value of the breaking loads is xm = 269,9 and
the variance = (103/104) s x 2 =755,70.
The best estimates for μ = 269,9 and for σ = 27,49. ( Sqrt(755,70)
The number of degrees of freedom ν = K - r -1. [K = 11
r = 2 -as two population parameters have been estimated ]
Therefore ν = 1 - 2 - 1 = 8
The value of c for P(χ 2 ≤ c) = (1 - α =0,95 ) from the table above = 15,507
The calculations in the table below yields a χ 2 = 9,003 which is less than 15,507.
Therefore the
the hypothesis that the population is normal is accepted.
| x j | 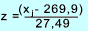 |
Φ (z) | e j = 104p j | b j |
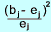 |
-  |
225 |
-  |
-1,6333 |
0 |
0,0516 |
5,3664 |
5 |
0,025 |
| 225 |
235 |
-1,6333 |
-1,2696 |
0,0516 |
0,102 |
5,2416 |
8 |
1,4516 |
| 235 |
245 |
-1,2696 |
-0,9058 |
0,102 |
0,1814 |
8,2576 |
13 |
2,7236 |
| 245 |
255 |
-0,9058 |
-0,542 |
0,1814 |
0,2946 |
11,7728 |
13,5 |
0,2534 |
| 255 |
265 |
-0,542 |
-0,1782 |
0,2946 |
0,4286 |
13,936 |
17,5 |
0,9115 |
| 265 |
275 |
-0,1782 |
0,1855 |
0,4286 |
0,5714 |
14,8512 |
13 |
0,2308 |
| 275 |
285 |
0,1855 |
0,5493 |
0,5714 |
0,7088 |
14,2896 |
9 |
1,9581 |
| 285 |
295 |
0,5493 |
0,9131 |
0,7088 |
0,8186 |
11,4192 |
9 |
0,5125 |
| 295 |
305 |
0,9131 |
1,2768 |
0,8186 |
0,898 |
8,2576 |
5,5 |
0,9209 |
| 305 |
315 |
1,2768 |
1,6406 |
0,898 |
0,9495 |
5,356 |
5,5 |
0,0039 |
| 315 |
+ 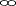 |
1,6406 |
+  |
0,9495 |
1 |
5,252 |
5 |
0,0121 |
|
χ 2 =9,0034 |
|