Introduction
A permutation is an arrangement of things with the order being important. abcd is different
to bcda. A combination is a selection of things e.g. abcd is the collection of the four letters with
no relevance given to the order. If a team of eleven players are selected for a football
team out of a selection of 20 persons with no importance given to the positions then the selection is
combination. However if each position (goalkeeper, left fullback etc. ) is chosen seperately
then the selection is a permutation.
Symbols..
n P(r) or n P (r) = Permutation of n items taken r at a time
n C(r) or n C (r) = Combination of n items taken r at a time
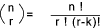
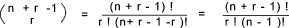
|
Permutations and combinations
Permutations: (Without Repitition)
Permutation illustrates the number of ways to arrange elements in a definite order.
The number of permutations of n items taken all at a time =
n! = 1.2.3 .....n (N Factorial)
The number of permutations of n elements of same kind taken r at a time.
nP(r) = n ! /(n-r)!
Example
The number of permutations of four l
etters a,b,c,d arranged three at a time is
4! /(4-3)! = 4.3.2.1 / 1 = 24
a,b,c / a,b,d /a,c,b /a,c,d / a,d,b/ a,d,c
b,a,c / b,a,d /b,c,a /b,c,d / b,d,a /b,d,c
c,a,b /c,a,d / c,b,a / c,b,d / c,d,a / c,d,b
d,a,b / d,a,c / d,b,a/ d,b,c / d,c,a /d,c,b
| Permutation Table (without Repetition) |
| n |
r |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 2 |
2 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 3 |
3 |
6 |
6 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 4 |
4 |
12 |
24 |
24 |
0 |
0 |
0 |
0 |
0 |
0 |
| 5 |
5 |
20 |
60 |
120 |
120 |
0 |
0 |
0 |
0 |
0 |
| 6 |
6 |
30 |
120 |
360 |
720 |
720 |
0 |
0 |
0 |
0 |
| 7 |
7 |
42 |
210 |
840 |
2520 |
5040 |
5040 |
0 |
0 |
0 |
| 8 |
8 |
56 |
336 |
1680 |
6720 |
20160 |
40320 |
40320 |
0 |
0 |
| 9 |
9 |
72 |
504 |
3024 |
15120 |
60480 |
181440 |
362880 |
362880 |
0 |
| 10 |
10 |
90 |
720 |
5040 |
30240 |
151200 |
604800 |
1814400 |
3628800 |
3628800 |
Permutations: (With Repetition)
A Permutation with repetition is the number of ways to arrange
elements in a definite order allowing elements to be repeated.
The number of permutations with repetition of n items taken r at a time =
nP(r) (with repetition) = n r
Example
The number of permutations of three
letters a,b,c arranged two at a time is
3 2 = 9
a,a / a,b / a,c / b,b /b,a / b,c/ c,c /c,a / c,b
| Permutation Table (With repetition) |
| n |
r |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 2 |
2 |
4 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 3 |
3 |
9 |
27 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 4 |
4 |
16 |
64 |
256 |
0 |
0 |
0 |
0 |
0 |
0 |
| 5 |
5 |
25 |
125 |
625 |
3125 |
0 |
0 |
0 |
0 |
0 |
| 6 |
6 |
36 |
216 |
1296 |
7776 |
46656 |
0 |
0 |
0 |
0 |
| 7 |
7 |
49 |
343 |
2401 |
16807 |
117649 |
823543 |
0 |
0 |
0 |
| 8 |
8 |
64 |
512 |
4096 |
32768 |
262144 |
2097152 |
16777216 |
0 |
0 |
| 9 |
9 |
81 |
729 |
6561 |
59049 |
531441 |
4782969 |
43046721 |
387420489 |
0 |
| 10 |
10 |
100 |
1000 |
10000 |
105 |
106 |
107 |
108 |
109 |
1010 |
Combinations:
A combination is the number of ways to arrange elements with
no definite order. The number of combinations of n elements of same kind taken r at a time.
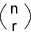
Equals
n C(r) = n ! / r !(n-r)!
Example.
The number of combinations of four letters a,b,c,d arrange three at a time is
4! / 3!(4-3)! = 4.3.2.1 / 6.1 = 4
a,b,c / a,b,d /a,c,d /b,c,d
| Combination Table (without Repetition) |
| n |
r |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 2 |
2 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 3 |
3 |
3 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 4 |
4 |
6 |
4 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
| 5 |
5 |
10 |
10 |
5 |
1 |
0 |
0 |
0 |
0 |
0 |
| 6 |
6 |
15 |
20 |
15 |
6 |
1 |
0 |
0 |
0 |
0 |
| 7 |
7 |
21 |
35 |
35 |
21 |
7 |
1 |
0 |
0 |
0 |
| 8 |
8 |
28 |
56 |
70 |
56 |
28 |
8 |
1 |
0 |
0 |
| 9 |
9 |
36 |
84 |
126 |
126 |
84 |
36 |
9 |
1 |
0 |
| 10 |
10 |
45 |
120 |
210 |
252 |
210 |
120 |
45 |
10 |
1 |
Combinations: with repetition
Combinations with repetition are the number of ways to arrange elements
with no definite order but the elements can be repeated. The number of combinations of n elements of same kind taken r at a time.
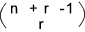
Equals
n C(r) = (n + r -1)! / r ! (n - 1)!
Example.
The number of combinations of four letters a,b,c arrange
two at a time is
(3 + 2 - 1)! / (2)!.(3-1)! = 4.3.2.1 / (2.1)(2.1) = 6
a,a /a,b / a,c / b,b / b,c/ c,c /
| Combination Table (with repetition) |
| n |
r |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 2 |
2 |
3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 3 |
3 |
6 |
10 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 4 |
4 |
10 |
20 |
35 |
0 |
0 |
0 |
0 |
0 |
0 |
| 5 |
5 |
15 |
35 |
70 |
126 |
0 |
0 |
0 |
0 |
0 |
| 6 |
6 |
21 |
56 |
126 |
252 |
462 |
0 |
0 |
0 |
0 |
| 7 |
7 |
28 |
84 |
210 |
462 |
924 |
1716 |
0 |
0 |
0 |
| 8 |
8 |
36 |
120 |
330 |
792 |
1716 |
3432 |
6435 |
0 |
0 |
| 9 |
9 |
45 |
165 |
495 |
1287 |
3003 |
6435 |
12870 |
24310 |
0 |
| 10 |
10 |
55 |
220 |
715 |
2002 |
5005 |
11440 |
24310 |
48620 |
92378 |
|