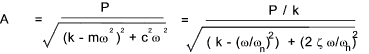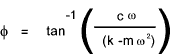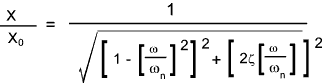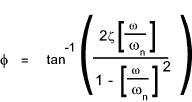|
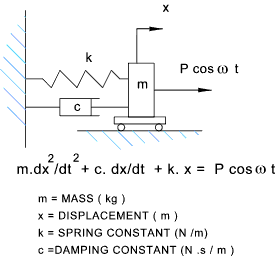
Steady State Forced Vibrations On the page Ref..Forced Vibrations covering vibration of a mass (m) with a k spring stiffness and c viscous damping
subject to a sinusoidal force of P cosω t.
x = A cos ( ω t - φ ) The modulus A was shown to be
The phase angle φ was shown to be
using the following derived relationships..
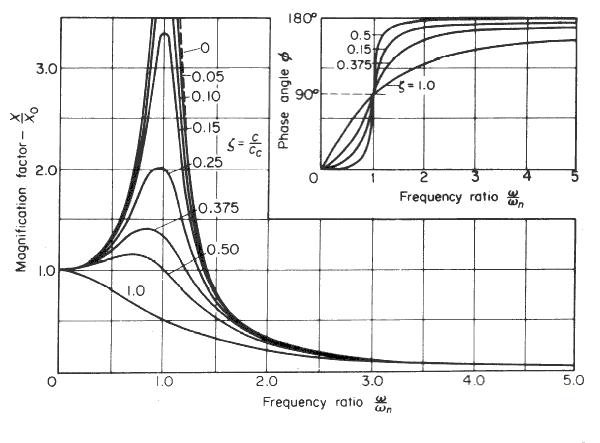
The dimensionless relationship between the Static displacement P/k (= Xo )and the Peak amplitude X is provided by the following
expression
The phase angle can be related to the driving frequency and the natural frequency
 Rotating Unbalanced Mass For the case of a mass M supported on springs k with viscous damping c which is supporting a rotating
unbalanced load of mass m rotating with and angular frequency ω at a radius r .
The peak amplitude and phase are provided by the following dimensionless expressions 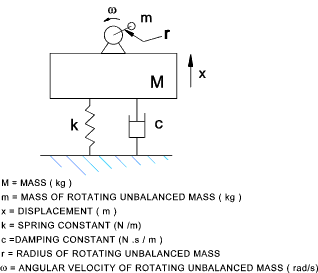 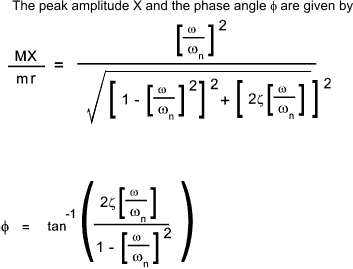 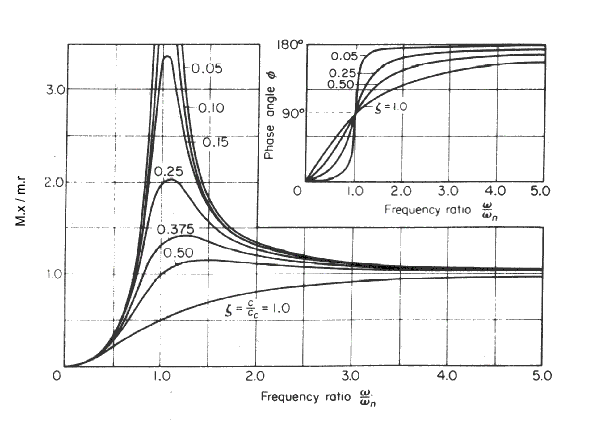 Excitation of Base For the case of a mass m supported on springs k with viscous damping c on a base which is moving
with an excitation of form y = Y sin ω t . 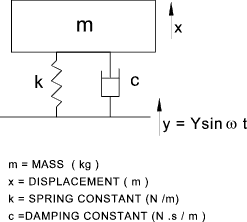 The ratio of peak ampltude of the mass and the base and the phase are provided by the following dimensionless expressions 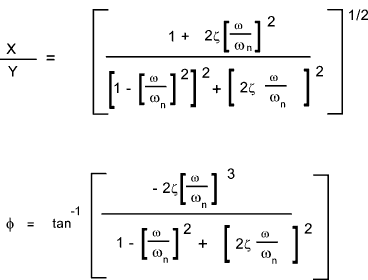 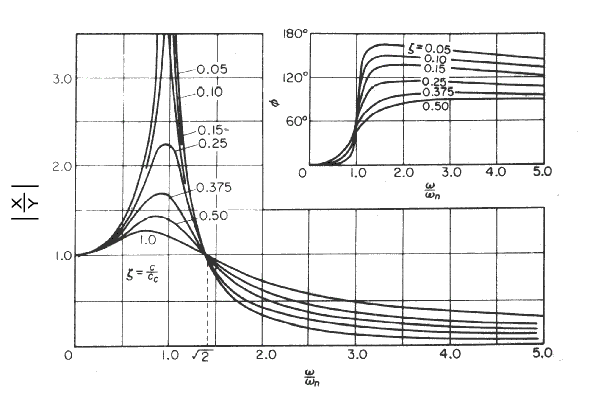 |
Links on Free Vibrations
|
|