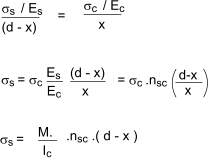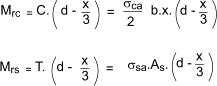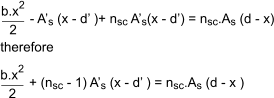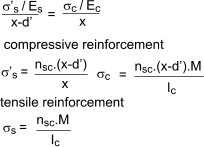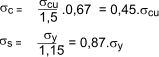This page includes note covering the theory of reinforced concrete beams.     The theory generally used in the past has bee based on elastic method of analysis.    In the last twenty years the elastic theory has beean superseded by the ultimate load method in the codes applicable to the construction industry.    The notes below consider , in outline, both methods.

The basis of this theory is provided on webpage Composite beams

Consider a rectangular beam subject to bending forces such that here are compressive forces on the top surface and tensile force on the bottom surface.     The beam is subject to a bending moment M and is reinforced in its tensile region by a number or reinforcement bars of total cross section are A_s. The centre of the reinfocement is at a depth d from the upper surface and is identified as the effective depth.    The neutral axis of the section is at a depth x from the upper surface.    The position of the neutral axis is to be calculated.    The concrete is assumed to only contribute to the strengh resisting bending in the compressive region above the neutral axis i.e all tensile forces are resisted by the steel reinforcement.

The modular ratio n_sc = E_s /E_c. Multiplying the area of the reinforcement bars by the modular ratio results in the area reinforcement being effectively transformed into an equivalent area of concrete....Taking moments of areas about the neutral axis results in the equation

This when rearranged results in the quadratic

The only relevant solution to this equation is the positive value

The second moment of area I_c of the transformed section is

The maximum stress in the concrete at the extreme fibre is

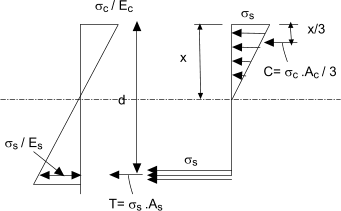
The strain diagram shown above may be used to calculate the stress in the reinforcement.    The strain diagram is linear throughout the depth since the beam section is assumed to remain plane during bending. Therfore

Moment of Resistance of beam

This is the moment withstood by the beam when the stress in the concrete or the steel reaches the maximum allowable value.    The value for the concrete and steel is calculated easily from the stress diagram

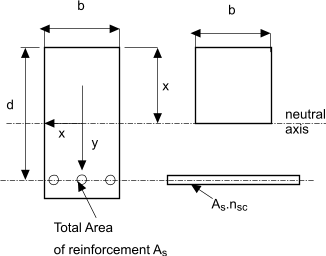
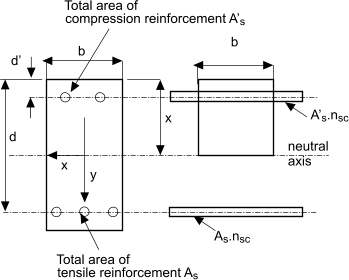
The moment of resistance of the beam according to elastic theory is the lesser of M_rc or M_rs

The critical /economic section of a beam is when the reinforcement area is adjusted such that M_rs is equal to M_rc

Reinforcement in compression zone of beam

For a beam of given cross section dimensions there is a point when increasing the area of the reinforcement does not provide a resulting increase in the moment of resistance because the concrete becomes the limiting factor.    This limitation can be overcome by adding reinforcement in the compression zone of the beam.     Consider a beam as shown below

Taking moments of area about the neutral axis

The second moment of area of the transformed section is therefore

The maximum stress in the concrete at the extreme fibre is

Ultimate load theory for concrete beams is based on the calculated moment of resistance (ultimate moment of reistance) being based on the failure strength of concrete in compression and the yield strength of the reinforcement of the steel in tension both modified by a margin of safety.     However concrete generally fails suddenly while the failure of steel is generally progressive .    The margins are typically 1,5 for concrete and 1,15 for steel.    When the characteristic stength for concrete is based on the cube strength it is necessry that it is multiplied by 2/3 because the stength in bending is always significantly less than that resulting from the cube strength.

The design strength for concrete and steel in bending is therefore typically

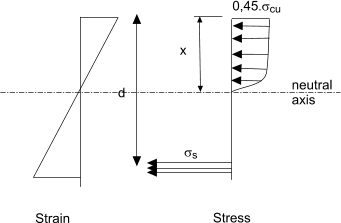
The ultimate load theory analysis is based on the assumptions that plane surfaces remain plane during bending and there is no contribution to the bending strength of the beam from concrete in tension.    The strain therefore varies uniformly down the beam section.    The stress diagram however is not linear but has a rectangular parabolic shape as shown below.

A reasonably accurate approximation of this curve which is used in strength calculations is shown below

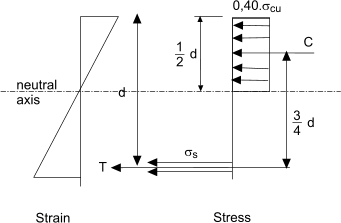
The moment of resistance in this instance is identified as the ultimate moment of resitance M_u and is easily calculated as shown below

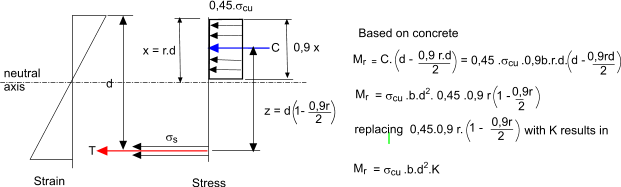
The section considered above identifies the ultimate moment of resistance when the neutral axis is 0,5.d .  A lower design moment would have a requirement for a section with a reduced value of x to the neutral axis.     It is easily possible by evaluating moment of resistance of a section resulting from different values of the ratio of x/d by taking moments about the tensile reinforcement.   
Note:The stress distribution, as used in the relevant code and as used for this exercise, is actually slightly different from that shown above.

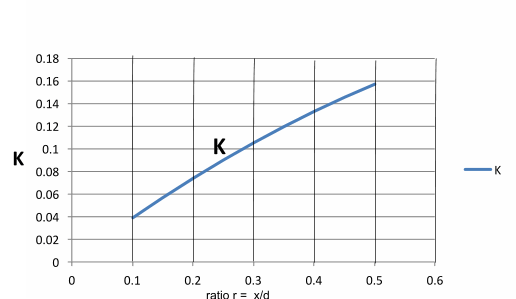
A plot of K vs r= x/d is easily plottted