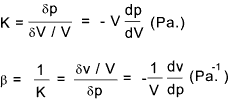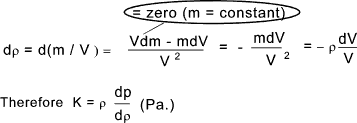Fluids can be either liquids or gases. A liquid is hard to compress and takes the shape of the vessel containing it. However it has a fixed volume and has an upper level surface.   Gas is easy to compress, and expands to fill its container. There is thus no free surface.  Liquids are generally assumed to be incompressible fluids and gases compressible fluids.   Liquids ar only compressible when they are highly pressurised, and the compressibility of gases may be disregarded whenever the change in pressure is very small.

Important characteristics of fluids from the viewpoint of fluid mechanics are density, pressure, viscosity, surface tension, and compressibility.  This section includes brief notes on these important characteristics.

The mass per unit volume of material is called the density, which is generally expressed by the symbol ρ. The density of a gas changes according to the pressure, but that of a liquid may be considered constant unless the relevant pressures changes are very high   The units of density are kg/m³ (SI).

The ratio of the density of a material ρ to the density of water ρ_w ( at 4^o C ) , is called the relative density(RD).    This is often called the specific gravity (sg) a term which is sometimes confusing..

Note: The for liquids and solids the specific gravity is generally identified as the ratio of the materials density relative to water both at the same conditions i.e 4^o and 1,013 bara ambient pressure.    For gases the specific gravity is the ratio of the materials density to the the density of air, both at the same conditions as identified above.    The term specific gravity is not as clear at term as the relative density.

For a liquid RD = ρ /ρ_w 
For a gas RD = ρ /ρ_a 

The apparent specific gravity sg_a is the ratio of the weight of a volume of a material to the weight of an equal volume of the reference fluid (water or air) again under the same conditions.     This is a practical value but essentially is the same as the true specific gravity.

The density of gases gases and vapours are greatly affected by the pressure .  For so called perfect gases the density can be calculated from the formula .

R_o = the universal Gas constant = 8314 J/(kg.K) and M = Molecular weight.    Therefore R = 8314/M   [ J/(kg.K) ]

The reciprocal of density, i.e. the volume per unit mass, is called the specific volume, which is generally expressed by the symbol υ

υ = 1/ρ

The dimensional formula for density = ML^-3 and the dimensional formula for specific volume = M^-1L³

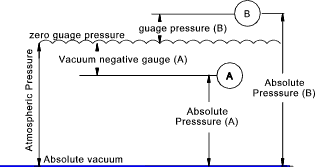
A fluid is always subject to pressure. Pressure is the force per unit area at a point.  The absence of pressure occurs in a complete vacuum.  A complete vacuum is really a theoretical concept.

The normal pressure experienced on the surface of the earth is called the atmospheric pressure and, in general, pressures are measured relative to the local atmospheric pressure.  These measured pressures are called gauge pressures.  The absolute pressure is the pressure relative to that of a perfect vacuum .  

The figure below shows the relationship between the gauge pressure and the absolute pressure for two measurements : a pressure less than atmospheric (A) and a pressure greater than atmospheric (B) are shown .

p_abs = p_gauge + p_atm

The SI unit of pressure is the Pascal (abrev.= Pa) (Newton /m² ).  The dimensional formula for pressure is ML^-1T^-2.

In considering fluid pressures it has been found convenient in hydrostatics and in fluid dynamics to use fluid head as a method of measuring pressure.   Considering the figure below.   A quantity of fluid in an open vessel is experiencing an atmospheric pressure on its surface.    A tube is routed vertically to a sealed container held at a pressure of absolute zero.

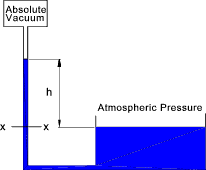
The liquid will be forced up the tube until the gravity force resulting from the level of fluid in the tube balances the force due to the pressure at the bottom of the head of fluid.  Assuming the area of the tube is A _t, the density of the fluid = ρ,and the pressure at the top of the tube is zero.    The force at x-x

F_xx = 0 + hAρg.

The pressure at x-x=

P_xx = 0 + hAρg. / A = hρg.

For a fluid with a known fixed density the height h can be conveniently used to identify the pressure.  For water the atmospheric pressure is about 10,5m.  In practice water vaporises into the vacuum at the top of the tube reducing the vacuum this reduces the column height by about 180mm.  

Mercury is used for measuring pressure and the height of a column of mercury which can be supported by atmospheric pressure is about 0,760m.  Mecurey has a low vapour pressure and the vacuum is only reduced by about 0,16 Pa, (very small compared to atmospheric pressure of 10⁵ Pa ).   It is clear that gauge pressures and vacuum pressures are easily obtained using this method.  The barometer identifies pressure readings in mm Hg.

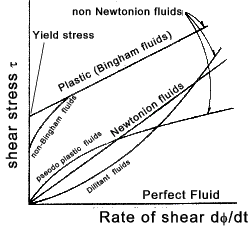
Additional ref notes.. Viscosity
Tables of fluid viscosities Fluid Viscosities

Perfect fluids cannot in theory transmit shear stresses.   All real fluids resist shear flow.  The viscosity property of the fluid defines the degree of resistance to flow it possess.  This is illustrated using the figure below.  A cylinder is located on a shaft and the space between is filled with a fluid.  The cylinder is rotated at an angular velocity ω.   The velocity distribution in the fluid as shown.   The torque required to rotate the cylinder is an indication of the viscosity of the fluid.

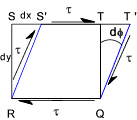
Consider an element of fluid STQR which is subject to a shear stress τ

In a short period of time dt the fluid element distorts to S'T'QR.   The fluid will experience a strain φ in time dt.  

μ ( dφ /dt ) = μ τ

Note: The rate of shear strain is also measured as the deflection dx divided by the distance dy i.e dx/dy occuring over a time intervel dt.  It is is effectively the velocity gradient dv /dy .. (dv = dx/dt)

= μ (dv/dy) = τ   ....   therefore  .....    μ = τ / (dv/dy)

If the element where an elastic solid it would distort a fixed amount proportional to the shear stress and the proportionality constant is called the Modulus of Rigidity (G).   The fluid element distorts at a rate based on the viscosity of the fluid.

The SI unit for viscosity is the Pa.s (Pascal Second).   This is simply derived from the units pressure /( velocity/ length) = Pa / (m /s / m )= Pa.s.  The dimensional formula = ML^-1T ^-1.   The centipoise , a cgs unit, is commonly used because water has a viscosity of 1,0020 cP (at 20 �C;). 1 cP = 10^-2 Poise.  1 Poise = 1g.cm.s^-1 = 0,1 Pa.s........ Therefore 1 Pa.s = 1000cP

Kinematic viscosity
The viscosity μ and the density ρ are both properties of a fluid.  The ratio μ/ρ is called the kinematic viscosity and is also a property.  Kinematic viscosity .ν can be completely defined in terms of length and time and has a dimensional equation L²T^-1.   The SI units for kinematic viscosity is the (m²�s^-1).    The cgs physical unit for kinematic viscosity is the stokes (abbreviated S or St).   It is sometimes expressed in terms of centistokes (cS or cSt).

1 centistokes stokes = 10^-2 stokes.  ...  1 stokes = 10^-4 m��s^-1.

Newtonion /Non-Fluids
Solids which distort an amount which is proportional to the stress are called elastic solids.   Fluids which deform at a rate which is proportional to the tangential stress are called Newtonion fluids.   Fluid mechanics generally relates to Newtonion fluids.    Fluid with high viscosities are called thick or heavy fluids and include tar, treacle and grease. Fluids of low viscosity are called thin fluids and include water, paraffin and petrol.  Gases have very low values of viscosity.   Non Newtonion fluids are studied under the heading of rheology.

Typical Non-Newtonion fluids include.

Pseudo plastic fluids e.g. solutions including gelatine, clay, milk and blood often have reduced viscosity when the rate of shear is increased.

Some fluids experience increased viscosity when the rate of shear is increased.  This group includes concentrated solutions of sugar, and aqueous suspensions of starch.

Some materials, including metals, deform continuously with little increase in stress when stessed above their yield point.  These behave as plastically above the yield point.

The surface of a liquid is the interface between the liquid volume and the fluid above the liquid.  Generally the liquid is water and the fluid above the liquid is air.  The molecules within the liquid attract each other and at the interface there are more attractive forces towards the bulk of the liquid than there are towards the adjacent gas molecules.  The molecular forces tend to pull into the fluid bulk.   The surface of a liquid is apt to shrink, and its free surface is in such a state that each section pulls another as if an elastic film is being stretched. The surface behaves like a flexible membrane.   This property is evident when overfilling a cup with water.   The level of water in the cup will be higher than the cup edge before it overflows.

If a double line is drawn on the surface of a liquid there is a force normal to the lines holding the lines together.

The tensile strength per unit length of assumed section on the free surface is called the surface tension (symbon γ).

For large volumes of liquid the forces due to gravity and inertia are large compared to the surface tension forces.  Therefore the surface tension is not considered in most hydrostatic and hydrodynamic calculations.

For small volumes and areas of fluid the surface tension becomes important and results in spherical water droplets and the capillary effect.

The volume of a fluid changes from V to V + δV as a result of the applied pressure changing from p to p + δp.   The compressibility (β) is basically (δV / V ) /δp   i.e. the ratio of the proportional change of volume to change of pressure .  This is the reciprocal of the bulk modulus K.   The bulk modulus K is similar to the spring factor , that is K .(δV/V) = δp

The volume of the fluid clearly decreases if the pressure increases and is proportionate assumed that the fluid does not change state during the process (it remains a liquid, solid or gas.

For water of normal temperature/pressure K = 2,06 x 10⁹ Pa, and for air K = 1.4 x l0⁵ Pa assuming adiabatic change.   In the case of water, 1/K = 4.85 x l0^-10Pa^-1.Water compresses by about 0.005% when the pressure is increased by 1 atm (10⁵ Pa).

The product of density ( ρ) and volume is the mass i.e. ρ V = m = constant.  , and therefore volume V = m /ρ.   The bulk modulus can be expressed in terms of density explained below

For gases the bulk modulus is very much dependent on the conditions : if the compression takes place at constant temperature the bulk modulus is called the isothermal bulk modulus and if the compression takes place with no transfer of heat across the system boundary the bulk modulus is colled the isentropic bulk modulus. The ratio of isentropic/isothermal bulk modulii is γ which is the ratio of specific heats.

The propagation speeds of traveling waves are characteristic of the media in which they travel and are generally not dependent upon the other wave characteristics such as frequency, period, and amplitude.   The speed of sound in air and other gases, liquids, and solids is predictable from their density and elastic properties(bulk modulus).   In a fluid medium the wave speed takes the general form

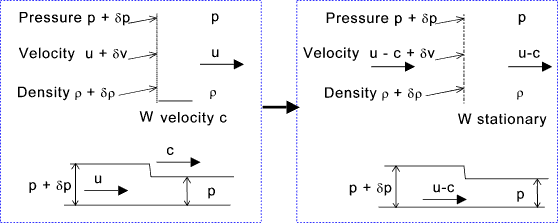
Consider a fluid in which a sound wave is being transmitted at a velocity c.  The fluid velocity is u.  To simplify the assessment this has been resolves such that the wave is stationary and the fluid has a velocity u-c.  See figure below.

Taking a small area normal to the wave front ΔA continuity requires that

.....(equation a)

For the volume enclosed by ΔA

the force to the right = (p + δ p)ΔA -pΔA

= The rate of increase of momentum towards the right

= ρ(u-c)ΔA (- δ u)

Therefore ...δp = ρ(c - u)δ u.....(equation B)

Elimination of δ u from (A) and (B) above

For a weak pressure wave with δp and δρ --> zero

This equation states that a sound wave which is a weak pressure surge of value √(∂ p /∂ ρ ) move through a fluid at a velocity of
( c-u ) =a (the speed of sound ) relative to the fluid ahead of it moving with a velocity u.   The assumption is that the friction is low and the resulting temperature difference across the wave is small.  The movement of the wave is considered to be isentropic.  (not heat transfer and no friction).

Now the bulk modulus is defined (see above) in terms of density by K = ρ ( ∂ p /∂ ρ )and therefore

Considering gases subject to isentropic processes. The law pv^γ = constant (k) applies. Therefore

The bulk modulus as defined above K = - v.(dp/dv) and therefore

K = γp and therefore for a perfect isentropic gas

The mach number M is the ratio of the velocity of gaseous flow in relation to the sonic velocity

Fluids velocities less than the speed of sound are called sub-sonic (M < 1) and fluid velocities greater than the speed of sound are called supersonic (M >1 )