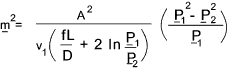Introduction
The notes below relate primarily to compressible fluids flowing in pipes. The notes are
of a basic level sufficient for a mechanical engineer to be able to estimate operating conditions
in a pipeline transferring vapours or gases.
It is much more difficult to determine the operating characteristics of compressible
fluids (vapours and gases) as the density is not constant under flowing conditions.
The extremes conditions encountered are adiabetic flow (PVγ = constant ) or isothermal flow (PV = constant).
Adiabetic conditions occur when no heat is transferred across system boundaries. Isothermal conditions
occur when the system changes occur at constant temperatures. For short
insulated pipes adiabetic conditions can be assumed. For long pipes
with reasonable levels of insulation isothermal conditions provide good approximations
to real conditions... Operating conditions occuring at some point between
the extremes can often be related to the polytropic process (PVn = constant)
Compressible fluid flows also have a maximum velocity which is limited by the speed of propogation
of a pressure wave travelling at the speed of sound for the fluid under consideration. If the differential
pressure along a pipe is such that the fluid velocity approaches sonic speed then any further increase
in differential pressure will not be accompanied by an increase in fluid velocity.
For many real life pipe flow conditions it is possible to use the Darcy equations and factors as provided
on webpage Pipe Flow Calcs subject to the following restrictions.
1).. If the calculated (estimated ) pressure drop (upstream (P1) - downstream (P2 ) is
less than 10% of the inlet pressure (P1) then reasonable accuracy is
achieved if the specific volume used is based on the known conditions. (Upstream or downstream).
2)..If the calculated (estimated ) pressure drop is greater than 10% but less than
about 40% of the inlet pressure P1 then reasonable accuracy is achieved by using
a specific volume based on the average of the downstream and upstream pressures.
3)..If the calculated (estimated) pressure drop is greater than 40% of P1 then methods as
identified on this page should be used.
Symbols
a = Acceleration (m/s2
A = Area (m2)
a = Speed of sound (m/s)
F = Force (N)
g = acceleration due to gravity (m/s2 )
h = fluid head (m)
K = Bulk modulus (MPa )
L = Pipe length (m )
m = mass (kg)
m = mass flow rate (kg/s)
M = mach number u /a
M = Molecular weight
P1 = Inlet fluid pressure (gauge) (N /m2 )
P2 = Outlet fluid pressure (gauge) (N /m2 )
P1 = Inlet fluid pressure (abs) (N /m2 )
P2 = Outlet fluid pressure (abs) (N /m2 )
P - Absolute pressure (N /m2 )
pgauge - gauge pressure (N /m2 )
patm - atmospheric pressure (N /m2 )
p s= surface pressure (N /m2 )
|
Q = Volume flow rate (m3 /s)
q = Heat transfer /unit mass (J/kg)
R = Gas Constant (J/(kg.K)
Ro = Universal Gas Constant (J/(kg.mol.K)
ρ = fluid density (kg /m2 )
s = specific volume (m3 /kg)
u = fluid velocity (m/s)
v = specific volume (m3/kg)
v1 = specific volume at inlet conditions(m3/kg)
x = depth of centroid (m)
β = Compressibility (1/MPa)
θ =slope (radians)
ρ = density (kg/m3)
ρ r = density (kg/m3)
τ = shear stress (N /m2)
μ = viscosity (Pa.s)
ν kinematic viscosity (m2�s-1)
υ = Specific volume (m3 / kg)
γ= Ratio of Specific Heats
|
Compressible Fluid Flow equations.
The flow of compressible fluids in long lines approximates
isothermal conditions. The flow rate in a pipe under isothermal
conditions is provided by the equation below...
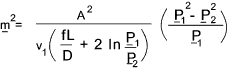
This equation has been developed on the basis of a number of assumptions including: Isothermal flow, steady flow, perfect gas laws apply,
constant friction value, straight and horizontal pipe. The equation below is a simplified version
and assumes no acceleration along streamlines.
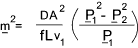
Limiting Flows.
The equations above do not take into account the fact that , for
a particular fluid, there is a maximum speed which cannot be exceeded in the compressible
fluid flowing in a pipe.
The maximum velocity of a compressible fluid is limited by the velocity of a pressure wave
travelling at the speed of sound in the fluid. Reference Sonic velocity.
Clearly the maximum velocity will be at the downstream end of the pipes as the velocity
will progressively rise as the pressure falls resulting in a increase in the specific volume. Now if the pressure drop is
sufficiently high such that sonic velocities is about to be exceeded
the resulting pressure decrease and hence driving force will not be transmitted
upstream and consequently there will be no increase in flow rate.
The sonic velocity which cannot be exceeded is expressed as
vs = √ (γRT ) = √ (γP v )
More Notes to follow -March -2007
Table of Air Flows through sched 40 Piping.
Notes : Factors for other conditions..
1) For inlet pressures (p o) other than 7 bar gauge... [ Multiply table pressure drop value by 8,013/(p o + 1,013) ]
2) For inlet temperatures (t o) other that 15 deg C... [ Multiply table pressure drop values by (273 + t o ) / 288 ]
3) For Pipe sizes (d o ) other than sched 40 ( d 40 )... [ Multiply table pressure drop values by (d 40 /do ) 5 ]
4) Pressure drop is proportional to length. For pipe lengths l o other than 100m.... [ multiply table presuure drop by l o /100 ]
It is important to note that this table should only be used for crude estimates. For serious work then detailed
calculations should be used.
Pipe Sizes 1/8" to 2"
| Pressure drop of air in bars per 100m of schedule 40 commercial pipe |
Air Flow
m3/min
15 Deg C
1,013 bar abs | | Pipe Size (Sched. 40) |
| 1/8" |
1/4" |
3/8" |
1/2" |
3/4" |
1" |
1 1/4" |
1 1/2" |
2" |
Inches |
| 3 |
6 |
10 |
12 |
20 |
25 |
32 |
40 |
50 |
mm |
| 6,8 |
9,2 |
12,5 |
15,8 |
21 |
26,6 |
35,1 |
40,9 |
52,5 |
ID(mm) |
| 0,03 |
0,093 |
0,021 |
0,0045 |
- |
|
|
|
|
|
| 0,06 |
0,337 |
0,072 |
0,016 |
0,0051 |
|
|
|
|
|
| 0,09 |
0,719 |
0,154 |
0,033 |
0,011 |
|
|
|
|
|
| 0,12 |
1,278 |
0,267 |
0,058 |
0,018 |
|
|
|
|
|
| 0,15 |
1,942 |
0,405 |
0,087 |
0,027 |
0,0067 |
|
|
|
|
| 0,2 |
3,357 |
0,698 |
0,146 |
0,047 |
0,011 |
0,0035 |
|
|
|
| 0,3 |
7,554 |
1,57 |
0,319 |
0,099 |
0,024 |
0,0073 |
|
|
|
| 0,4 |
|
2,71 |
0,548 |
0,17 |
0,041 |
0,012 |
|
|
|
| 0,5 |
|
4,1 |
0,842 |
0,257 |
0,062 |
0,018 |
|
|
|
| 0,6 |
|
5,9 |
1,19 |
0,37 |
0,088 |
0,026 |
0,0066 |
|
|
| 0,7 |
|
8,03 |
1,62 |
0,494 |
0,117 |
0,035 |
0,0086 |
0,0041 |
|
| 0,8 |
|
|
2,12 |
0,634 |
0,15 |
0,044 |
0,011 |
0,0053 |
|
| 0,9 |
|
|
2,64 |
0,803 |
0,187 |
0,055 |
0,014 |
0,0065 |
|
| 1,0 |
|
|
3,26 |
0,991 |
0,231 |
0,067 |
0,017 |
0,0079 |
|
| 1,25 |
|
|
4,99 |
1,55 |
0,353 |
0,102 |
0,026 |
0,012 |
|
| 1,5 |
|
|
7,2 |
2,19 |
0,499 |
0,147 |
0,036 |
0,017 |
0,0048 |
| 1,75 |
|
|
9,79 |
2,98 |
0,679 |
0,196 |
0,047 |
0,022 |
0,0064 |
| 2,0 |
|
|
|
3,82 |
0,871 |
0,257 |
0,062 |
0,029 |
0,0082 |
| 2,25 |
|
|
|
4,84 |
1,1 |
0,325 |
0,076 |
0,036 |
0,01 |
| 2,5 |
|
|
|
5,97 |
1,36 |
0,393 |
0,094 |
0,045 |
0,012 |
| 3,0 |
|
|
|
8,6 |
1,92 |
0,565 |
0,135 |
0,063 |
0,018 |
| 3,5 |
|
|
|
|
2,61 |
0,754 |
0,184 |
0,086 |
0,024 |
| 4,0 |
|
|
|
|
3,41 |
0,984 |
0,236 |
0,11 |
0,03 |
| 4,5 |
|
|
|
|
4,32 |
1,25 |
0,298 |
0,136 |
0,038 |
| 5,0 |
|
|
|
|
5,34 |
1,54 |
0,368 |
0,164 |
0,046 |
| 6 |
|
|
|
|
7,68 |
2,17 |
0,518 |
0,236 |
0,066 |
| 7 |
|
|
|
|
|
2,95 |
0,689 |
0,321 |
0,09 |
| 8 |
|
|
|
|
|
3,85 |
0,9 |
0,419 |
0,115 |
| 9 |
|
|
|
|
|
4,88 |
1,14 |
0,53 |
0,145 |
| 10 |
|
|
|
|
|
6,02 |
1,41 |
0,64 |
0,179 |
| 11 |
|
|
|
|
|
7,29 |
1,71 |
0,774 |
0,217 |
| 12 |
|
|
|
|
|
8,67 |
2,02 |
0,921 |
0,252 |
| 13 |
|
|
|
|
|
|
2,38 |
1,08 |
0,295 |
| 14 |
|
|
|
|
|
|
2,76 |
1,25 |
0,343 |
| 15 |
|
|
|
|
|
|
3,13 |
1,44 |
0,393 |
| 16 |
|
|
|
|
|
|
3,57 |
1,64 |
0,443 |
| 17 |
|
|
|
|
|
|
4,01 |
1,85 |
0,5 |
| 18 |
|
|
|
|
|
|
4,49 |
2,07 |
0,558 |
| 19 |
|
|
|
|
|
|
5,01 |
2,31 |
0,618 |
| 20 |
|
|
|
|
|
|
5,49 |
2,53 |
0,685 |
| 22 |
|
|
|
|
|
|
6,65 |
3,07 |
0,825 |
| 24 |
|
|
|
|
|
|
7,91 |
3,61 |
0,982 |
| 26 |
|
|
|
|
|
|
9,28 |
4,22 |
1,15 |
| 28 |
|
|
|
|
|
|
|
4,86 |
1,33 |
| 30 |
|
|
|
|
|
|
|
5,62 |
1,52 |
| 32 |
|
|
|
|
|
|
|
6,39 |
1,73 |
| 34 |
|
|
|
|
|
|
|
7,22 |
1,94 |
| 36 |
|
|
|
|
|
|
|
8,09 |
2,17 |
| 38 |
|
|
|
|
|
|
|
|
2,41 |
| 40 |
|
|
|
|
|
|
|
|
2,67 |
| 45 |
|
|
|
|
|
|
|
|
3,36 |
| 50 |
|
|
|
|
|
|
|
|
4,15 |
| 60 |
|
|
|
|
|
|
|
|
5,98 |
| 70 |
|
|
|
|
|
|
|
|
8,14 |
| Inches |
1/8" |
1/4" |
3/8" |
1/2" |
3/4" |
1" |
1 1/4" |
1 1/2" |
2" |
| mm |
3 |
6 |
10 |
12 |
20 |
25 |
32 |
40 |
50 |
| ID(mm) |
6,8 |
9,2 |
12,5 |
15,8 |
21 |
26,6 |
35,1 |
40,9 |
52,5 |
Pipe Sizes 2 1/2" to 12"
| Pressure drop of air in bars per 100m of schedule 40 commercial pipe |
Air Flow
m3/min
15 Deg C
1,013 bar abs | | Pipe Size (Sched. 40) |
| 2 1/2" |
3" |
3 1/2" |
4" |
5" |
6" |
8" |
10" |
12" |
Inches |
| 3 |
80 |
90 |
100 |
125 |
150 |
200 |
250 |
300 |
mm |
| 62,7 |
77,9 |
90,1 |
102,3 |
128,2 |
154,1 |
202,7 |
254,5 |
303,3 |
ID (mm) |
| 2,25 |
0,0042 |
|
|
|
|
|
|
|
|
| 2,5 |
0,0051 |
|
|
|
|
|
|
|
|
| 3,0 |
0,0073 |
|
|
|
|
|
|
|
|
| 3,5 |
0,0097 |
|
|
|
|
|
|
|
|
| 4,0 |
0,012 |
|
|
|
|
|
|
|
|
| 4,5 |
0,016 |
0,0051 |
|
|
|
|
|
|
|
| 5,0 |
0,019 |
0,0063 |
|
|
|
|
|
|
|
| 6 |
0,027 |
0,009 |
|
|
|
|
|
|
|
| 7 |
0,036 |
0,012 |
0,0059 |
|
|
|
|
|
|
| 8 |
0,047 |
0,015 |
0,0075 |
|
|
|
|
|
|
| 9 |
0,058 |
0,019 |
0,0094 |
|
|
|
|
|
|
| 10 |
0,072 |
0,023 |
0,011 |
|
|
|
|
|
|
| 11 |
0,085 |
0,028 |
0,014 |
0,0073 |
|
|
|
|
|
| 12 |
0,101 |
0,033 |
0,016 |
0,0085 |
|
|
|
|
|
| 13 |
0,119 |
0,039 |
0,019 |
0,0098 |
|
|
|
|
|
| 14 |
0,138 |
0,045 |
0,022 |
0,011 |
|
|
|
|
|
| 15 |
0,158 |
0,051 |
0,025 |
0,013 |
|
|
|
|
|
| 16 |
0,178 |
0,058 |
0,028 |
0,015 |
|
|
|
|
|
| 17 |
0,2 |
0,065 |
0,031 |
0,016 |
|
|
|
|
|
| 18 |
0,223 |
0,072 |
0,035 |
0,018 |
|
|
|
|
|
| 19 |
0,247 |
0,081 |
0,039 |
0,02 |
|
|
|
|
|
| 20 |
0,266 |
0,089 |
0,043 |
0,022 |
0,0072 |
|
|
|
|
| 22 |
0,328 |
0,107 |
0,052 |
0,027 |
0,0086 |
|
|
|
|
| 24 |
0,388 |
0,126 |
0,061 |
0,032 |
0,01 |
|
|
|
|
| 26 |
0,455 |
0,148 |
0,071 |
0,037 |
0,012 |
|
|
|
|
| 28 |
0,525 |
0,171 |
0,082 |
0,043 |
0,014 |
0,0054 |
|
|
|
| 30 |
0,603 |
0,197 |
0,094 |
0,049 |
0,016 |
0,0061 |
|
|
|
| 32 |
0,682 |
0,222 |
0,106 |
0,055 |
0,018 |
0,0069 |
|
|
|
| 34 |
0,77 |
0,251 |
0,119 |
0,062 |
0,02 |
0,0078 |
|
|
|
| 36 |
0,863 |
0,28 |
0,134 |
0,07 |
0,022 |
0,0087 |
|
|
|
| 38 |
0,957 |
0,312 |
0,148 |
0,077 |
0,024 |
0,0096 |
|
|
|
| 40 |
1,05 |
0,346 |
0,164 |
0,086 |
0,027 |
0,011 |
|
|
|
| 45 |
1,33 |
0,435 |
0,207 |
0,107 |
0,034 |
0,013 |
|
|
|
| 50 |
1,65 |
0,534 |
0,254 |
0,132 |
0,042 |
0,016 |
|
|
|
| 60 |
2,37 |
0,765 |
0,363 |
0,188 |
0,059 |
0,023 |
0,0058 |
|
|
| 70 |
3,23 |
1,03 |
0,495 |
0,254 |
0,08 |
0,031 |
0,0077 |
|
|
| 80 |
4,22 |
1,35 |
0,639 |
0,332 |
0,104 |
0,04 |
0,01 |
|
|
| 90 |
5,34 |
1,7 |
0,808 |
0,418 |
0,13 |
0,051 |
0,013 |
0,0041 |
|
| 100 |
6,59 |
2,1 |
0,992 |
0,513 |
0,16 |
0,062 |
0,015 |
0,005 |
|
| 110 |
7,97 |
2,54 |
1,19 |
0,621 |
0,192 |
0,075 |
0,019 |
0,006 |
|
| 120 |
9,49 |
3,02 |
1,42 |
0,739 |
0,228 |
0,089 |
0,022 |
0,0071 |
|
| 130 |
|
3,55 |
1,67 |
0,862 |
0,267 |
0,103 |
0,026 |
0,0082 |
|
| 140 |
|
4,12 |
1,93 |
1 |
0,308 |
0,12 |
0,029 |
0,0095 |
|
| 150 |
|
4,73 |
2,22 |
1,15 |
0,353 |
0,138 |
0,034 |
0,011 |
0,0045 |
| 200 |
|
8,4 |
3,94 |
2,03 |
0,628 |
0,243 |
0,059 |
0,019 |
0,0078 |
| 250 |
|
|
6,16 |
3,17 |
0,975 |
0,378 |
0,09 |
0,029 |
0,012 |
| 300 |
|
|
8,88 |
4,56 |
1,4 |
0,54 |
0,129 |
0,041 |
0,017 |
| 350 |
|
|
|
6,21 |
1,9 |
0,735 |
0,174 |
0,056 |
0,023 |
| 400 |
|
|
|
8,11 |
2,48 |
0,96 |
0,227 |
0,072 |
0,03 |
| 450 |
|
|
|
|
3,14 |
1215 |
0,286 |
0,091 |
0,037 |
| 500 |
|
|
|
|
3,88 |
1,5 |
0,352 |
0,112 |
0,046 |
| 550 |
|
|
|
|
4,69 |
1,82 |
0,424 |
0,134 |
0,055 |
| 600 |
|
|
|
|
5,58 |
2,16 |
0,504 |
0,16 |
0,066 |
| 650 |
|
|
|
|
6,55 |
2,54 |
0,592 |
0,188 |
0,076 |
| 700 |
|
|
|
|
7,6 |
2,94 |
0,686 |
0,218 |
0,089 |
| 750 |
|
|
|
|
8,72 |
3,38 |
0,788 |
0,248 |
0,101 |
| 800 |
|
|
|
|
|
3,84 |
0,896 |
0,282 |
0,115 |
| 850 |
|
|
|
|
|
4,34 |
1,01 |
0,319 |
0,13 |
| Inches |
2 1/2" |
3" |
3 1/2" |
4" |
5" |
6" |
8" |
10" |
12" |
| mm |
3 |
80 |
90 |
100 |
125 |
150 |
200 |
250 |
300 |
| ID (mm) |
62,7 |
77,9 |
90,1 |
102,3 |
128,2 |
154,1 |
202,7 |
254,5 |
303,3 |
|