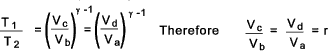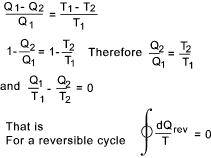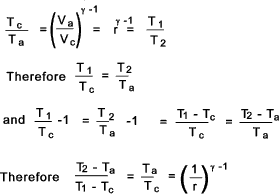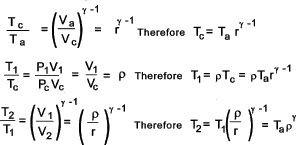Thermos Index Thermodynamics Cycles
| Introduction Various internal combustion engine types have been devised and represented by various idealised
cycles (otto cycle for four stroke, diesel cycle etc.. These idealised cycles
are useful for determining the practical limitations and efficiencies possible. They
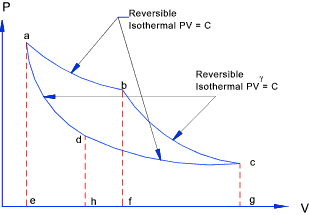
do not however provide the answer to the question.. Carnot Cycle Carnot in 1824 arrived at the "carnot cycle" which is an idealised gas
cycle that obtains the maximum amount of work from an engine working in a thermodynamically reversible manner. This cycle
provides a maximum efficiency for any thermodynamic heat engine
This imaginary working fluid is contained in the (cylinder)closed system and simply
receives and rejects energy to a source and sink using perfect heat transfer (with no
temperature difference ). As a result of receiving and rejecting energy it expands
and contracts during four ideal reversible "no-flow" processes. The fluid is an
ideal gas following the ideal gas laws.
The work done through during a complete cycle is determined using the relationships identified
on webpage Polytropic processes....
From the table it can clearly be seen that the total work done by the carnot cycle
is Rm(T1 - T1 )loge r = Q1 - Q2.
This is the maximum efficiency achievable by an reversible thermodynamic cycle working with a ideal perfect gas. The following relationship results from the above....
Air Standard cycles Although the Carnot cycle is theoretically the most efficient it is in no way a practical device.
Also the energy transfers would be far too slow for any real benefits to be realised.
Internal combustion engines work on non cyclic processes because the fuel-air mix enters the system and
products of combustion exit the system. . However theoretical cycles based on the
hypothesis that air is the working fluid in a closed system receiving an rejecting energy to external sinks allows provide
very crude estimations on the theoretical efficiencies possible internal combustion engines.
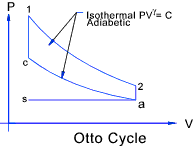
The Otto cycle is comprised of four reversible processes of air in a closed system:
The diagram for this process is shown above.
The thermal efficiency of and otto cycle is therefore.
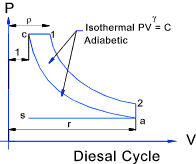
Diesel Cycle
This hypothetical cycle is one with heat being rejected at constant pressure. The stages of the cycle are shown below.
Energy supplied during c-1 = mcp (T1 - Tc )
This can be simplified as follows:
The Thermal efficiency is now simplified as follows...
|
Air Cycle Links
|
|
Thermos Index