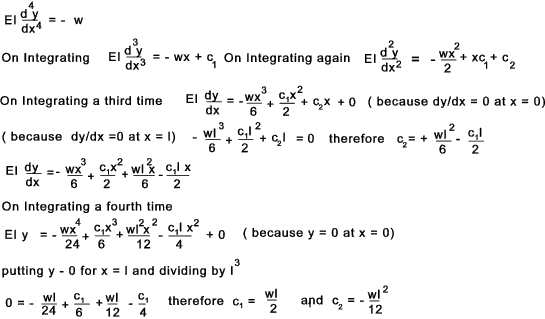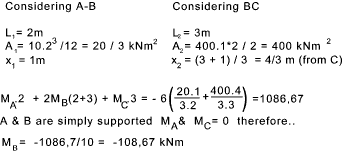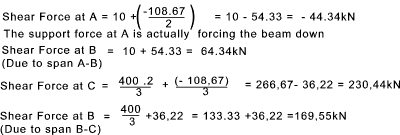|
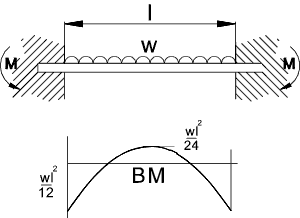
Introduction Built -in (Encastre) beams are fixed at both ends.
Continuous beams, which are beams with more than two supports and covering more
than one span, are not statically determinate using the static equilibrium laws.
e = strain Built in beams A built in beam is normally considered to be horizontal with both ends built-in at
the same level and with zero slope at both ends. A loaded built in beam
has a moment at both ends and normally the maximum moments at at one or both of the
two end joints.
It is not normally possible to determine the bending moments and the resulting stress using static equilibrium.
Deflection calculations are often used to enable the moments to be determined.
Using the above beam as an example...
Using the above equations the bending moment, shear force, deflection, slope can be determined at
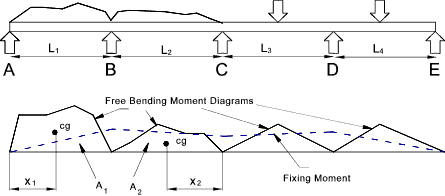
any point along the beam. M = EI d 2y/dx 2 = w(- 6x2+6lx -l2)/12 at x = 0 & l then M = -wl2 /12 and at x = l/2 then M = wl2 /24 Continuous Beams This type of beam is normally considered using the Clapeyron's Theorem ( Three Moments theorem)
The three moments theorem identifies the relationship between the bending moments found at three consecutive
supports in a continuous beam. This is achieved by evaluating the slope of of the beam
at the end where the two spans join. The slopes are expressed in terms of the three moments
and the supported loads which are then equated and the resulting equations solved.
If the beams has a different section for each span then the more general expression applies as shown below.
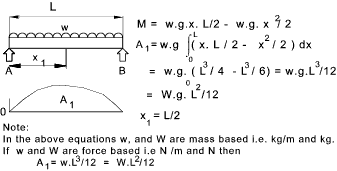
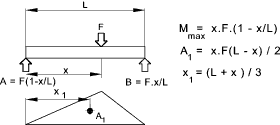
Example Areas and x 1 value calculations.
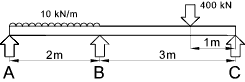
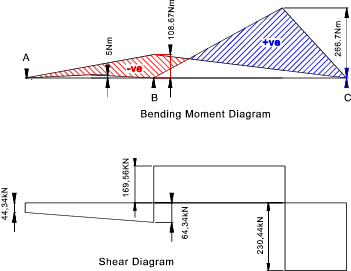
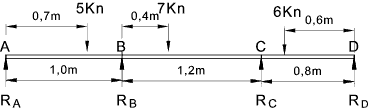
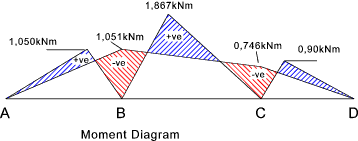
Examples using theorem. Example 1)
This simple example is a three span continuous beam with the ends simple supported,therefore with no moments at the end support points..
The values of A1,x1,A2, and x2 are calculated using the methods above..
|
Sites Providing Relevant Information
|
|