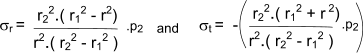Note: For more detailed stress & strain notes refer to webpage Stress & Strain

Strain = Change in length (dL)over original length (L)

e = dL / L

Stress = Force (F) divided by Area withstanding Force (A)

σ = F / A

Young's Modulus E = Stress ( s ) / Strain(e). This is a property of a material

E = s / e

General Formula for Bending


A beam with a moment of inertia I and with Young's modulus E will have a bending stress f at a distance from the Neutral Axis (NA) y and the NA will bend to a radius R ...in accordance with the following formula.

Simply Supported Beam . Concentrated Load

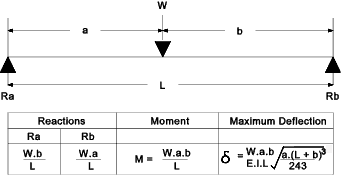Simply Supported Beam . Uniformly Distributed Load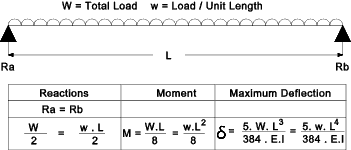

Cantilever . Concentrated Load

Cantilever . Uniformly Distributed Load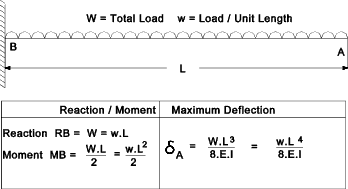

Fixed Beam . Concentrated Load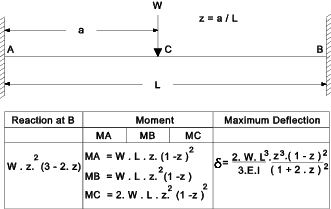

Fixed Beam . Uniformly Distributed Load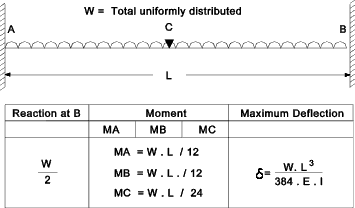

Poisson's Ratio = ν = (lateral strain / primary strain )

Shear Modulus G = Shear Stress /Shear Strain

G = τ / ε = E / (2 .( 1 + ν ))

General Formula for Torsion

A shaft subject to a torque T having a polar moment of inertia J and a shear Modulus G will have a shear stress q at a radius r and an angular deflection θ over a length L as calculated from the following formula.

T / J = G . θ / L = t / r

More detailed notes on torsion calculations are found at webpage Torsion

For a thin walled cylinder subject to internal pressure P the circumferential stress = σ_c

This stress tends to stretch the cylinder along its length. This is also called the longitudinal stress.

σ_c = P . d / ( 4 . t )

For a thin walled cylinder subject to internal pressure P the tangential stress = σ_c
This stress tends to increase the diameter). This is also called the hoop stress.

σ_t = P . d / ( 2 . t )

The above two formulae are only valid if the ratio of thickness to dia is less than 1:20

The equations for the stresses in thick walled cylinders are derived on web page Cylinders

r₁ = internal radius
r₂ =outer radius
p₁ = internal pressure
p₂ = external pressure
σ _r = radial stress
σ _t =tangential stress

Consider a cylinder with and internal diameter d ₁, subject to an internal pressure p ₁.  The external diameter is d ₂ which is subject to an external pressure p ₂.    The radial pressures at the surfaces are the same as the applied pressures therefore

σ _r = A + B / r ²
σ _t = A - B / r ²

The radial pressures at the surfaces are the same as the applied pressures therefore

- p₁ = A + B / r ₁²
-p₂ = A + B / r ₂²

The resulting general equations are known as Lame's Euqations and are shown as follows

If the external pressure is zero this reduces to

If the internal pressure is zero this reduces to