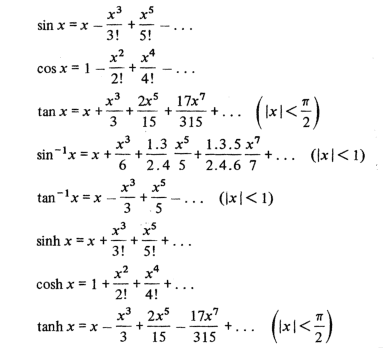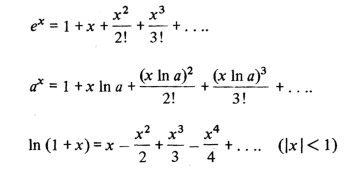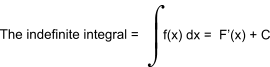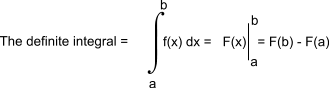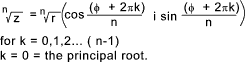Mensuration
Area of a Triangle, (sides a,b,c).. Area = ( b . c sin A )/ 2
Area of a Triangle = Sqrt (s .(s - a). (s - b). (s - c))........( s = (a + b + c)/ 2.)
Area of a Circle (r = radius).. Area = π . r 2
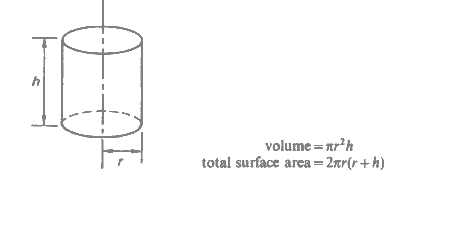
Area and Volume of a Cylinder
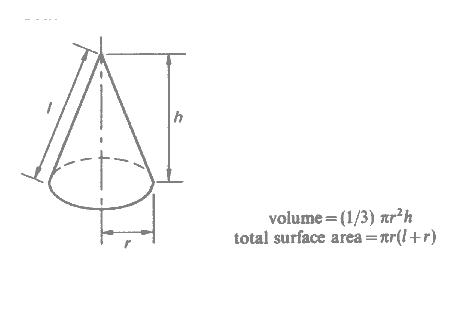
Area and Volume of a Cone
Area and Volume of a Frustrum of a Cone
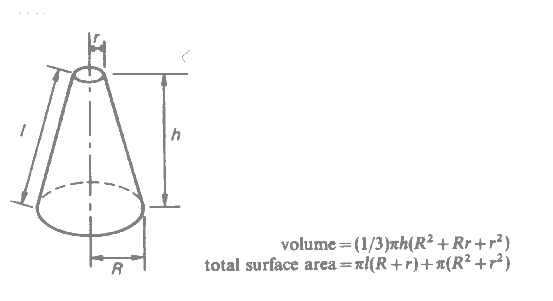
Area and Volume of a Sphere
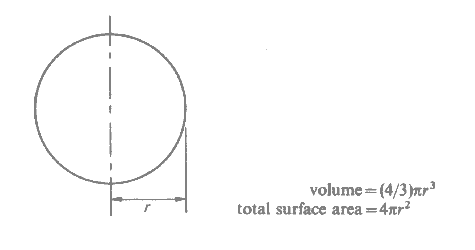
Area and Volume of a Pyramid
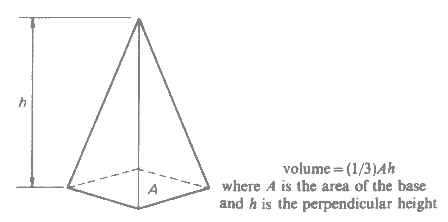
Trigonometry...
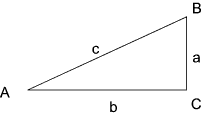
Definitions...
Sin A = Opposite / Hypotenuse = a / c
Cosine A = Adjacent / Hypotenuse = b / c
Tangent A = Opposite / Adjacent = a / b
Cosecant A = 1 / sin = c / a
Secant A = 1/cosine = c / b
Cotangent A = 1/tangent. = b / a
Trigonometric Relations...
Sin ( - A) = - Sin (A)
Cos ( - A) = cos (A)
Sin (A) 2 + Cos A 2 = 1
Cos (A) 2 =(1 + Cos (2A) ) /2
|
Trigonometric Relations...(continued)
Sin (A) 2 =(1 - Cos (2A) ) /2
Sin (A) Cos(A) = Sin (2A) /2
Sin (A + B) = Sin (A) Cos(B) + Cos(A) Sin(B)
Sin (A - B) = Sin (A) Cos(B) - Cos(A) Sin(B)
Cos (A + B) = Cos (A) Cos(B) - Sin(A) Sin(B)
Cos (A - B) = Cos (A) Cos(B) + Sin(A) Sin(B)
Sin(A).Sin(B) = [-Cos(A+B) + Cos (A-B)]/2
Cos(A).Cos(B) = [Cos(A+B) + Cos (A-B)]/2
1 + tan(A) 2 = sec(A) 2
1 + cot(A) 2 = cosec(A) 2
|
Hyperbolic Functions
sinh x = (e x - e - x) / 2
cosh x = (e x + e - x) / 2
tanh x = sinh x / cosh x = (e x - e - x) / (e x + e - x)
sech x = 1 / sinh x = 2 / (e x - e - x)
cosech x = 1 / cosh x = 2 / (e x + e - x)
coth x = cosh x / sinh x = (e x + e - x) / (e x - e - x)
|
ejx = cos x + j sin x
ex = cosh x + j sinh x
sin x = (e jx - e - jx) /2.j
cos x = (e jx + e - ix) /2
sin jx = j.sinh x
cos jx = cohs x
|
Quadratic Equation
A quadratic equation is generally of the form...
ax2 +b x + c = 0
The general solution of this equation is
x = ( - b ± Ö (b2 - 4 a c ) /2a
Expansions
The expansions below are developed using Taylors theorem
Trigonometric Expansions
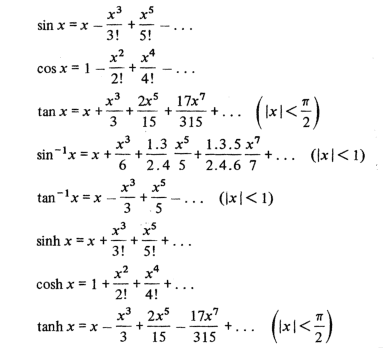
Exponential /Logarithmic Expansions
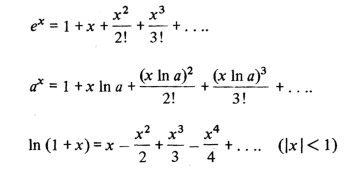
Derivatives..
| f (x) |
f '(x)= df(x) / dx |
| sin x |
cos x |
| cos x |
- sin x |
| tan x |
sec2 x |
| cotan x |
- cosec2 x |
| sec x |
sec x. tan x |
| cosec x ... |
- cosec x. cot x. |
| sinh x ... |
cosh x. |
| cosh x ... |
sinh x. |
| tanh x ... |
sech2 x. |
| cosech x ... |
- coth x cosech x |
| sech x ... |
- tanh x sech x |
| coth x ... |
- cosech 2 x |
| u .v |
u . dv/dx + v . du/dx |
| u / v |
(v . du / dx - u . dv / dx ) / v 2 |
| a. x n |
a. n . x n - 1 |
| e a x |
a . e a x |
| a x |
a x. ln a |
| x x |
x x /(1 + ln x) |
| ln x |
1 / x |
| log a x |
1 / x . log a e |
| sin - 1( x /a) |
1 / Sqrt(a 2 - x 2 ) |
| cos - 1( x /a) |
- 1 / Sqrt(a 2 - x 2 ) |
| tan - 1( x /a) |
a / (a 2 + x 2 ) |
Indefinite Integrals.....Integration by Parts
y = f(x) ...y is a function of x
F(x) is the integral of f(x)
The differentiation of F(x) results in f(x)
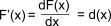
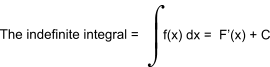
On differential the unknown constant C disapears.
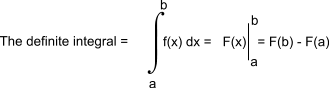
Table of Indefinite Integrals
| f(x) | 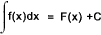 |
The constant of integration C is ommitted from the table of indefinite integrals below
| | | | |
| xa | x a+1 / (a + 1) |
| |
| 1 / (x 2 + a2) | (1 / a) . tan - 1 (x / a) |
| |
| 1 / (x 2 - a2) | (1 /2 a) . ln ( ( x - a ) /(x + a)) |
| |
| ( a + b x ) n (n not - 1) | (a + b x)n + 1 / b (n + 1) |
| |
| ( a + b x ) - 1 | 1 / b .ln ( a + b x ) |
| |
| x / (a x +b) | (a x + b - b ln(ax +b) ) / a2 |
| |
| 1 / x | ln x |
| |
| 1 / Sqrt (x 2 - a 2) | cosh - 1 (x / a) |
| |
| 1 / Sqrt (x 2 + a 2) | sinh - 1 (x / a) |
| |
| ex | ex |
| |
| 1 / ( a2 - x2) | (1 / a). tanh - 1 ( x / a ) = 1 /( 2. a) . log(a + x/a - x ) |
| |
| ax | ax / ln a |
| |
| x ax | (a x / ln a ) - (a x /( ln a ) 2 ) |
| |
| x ea x | e a x (a x - 1) / a2 |
| |
| 1 /(a + b e c x ) | (x / a) - ln (a + b ec x ) / a c |
| |
| ln x | x (ln x - 1 ) |
| |
| ( ln x )2 | x [ (ln x )2 - 2 ln x +2 ] |
| |
| 1 / x ln x | ln ( ln x ) |
| |
| sin x | - cos x |
| |
| cos x | sin x |
| |
| tan x | - ln cos x |
| |
| cotan x | ln sin x |
| |
| sec x | ln ( sec x + tan x ) = ln (tan (x/ 2 + π/ 4) ) |
| |
| cosec x | log | tan x/ 2 | |
| |
| 1 / Sqrt( x 2 + a 2) | sinh - 1( x / a ) = log ( (x/a) +Sqrt(x2 /a2 +1)) |
| |
| 1 / Sqrt( x2 - a 2) | cosh - 1( x / a ) |
| |
| 1 / Sqrt( a2 - x 2) | sin - 1( x / a ) |
| |
| sinh x | cosh x |
| |
| cosh x | sinh x |
| |
| tanh x | ln cosh x |
| |
| cosech x | ln tanh (x / 2 ) |
| |
| sech x | tan - 1 ( sinh x ) |
| |
| coth x | ln sinh x |
| |
| sinh 2 x | ( - x + ( sinh (2 x)) /2 ) / 2 |
| |
| cosh 2 x | ( x + ( sinh (2 x) ) /2 ) / 2 |
| |
| sech 2 x | tanh x |
| |
| cosech 2 x | - coth x |
| |
| tanh 2 x | x - tanh x |
Moments Of Inertia of Plane Sections
I = moment of Inertia about the identified axis.
J = Polar moment of inertia about the centroid of section
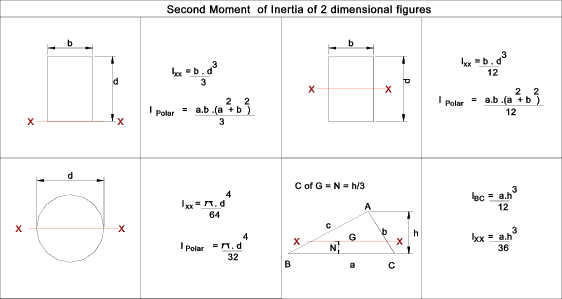
For More detailed information refer..
Properties of Plane Areas
Properties of solids
Parallel axis Theory..
If the second moment of an area (A) about an axis x - x = I xx.
Then the second moment of Area about a parallel axis y - y which is distance x from x - x =
I yy = I xx + A . x 2
Complex Numbers..
In mathematics it is necessary to provide a method of identifying the root of a
negative number i.e p = √ ( - 4). p is clearly not real
number it is an imaginary number.
Again an equation x2 - 2x +5 = 0 results
in (x - 1)2 = - 4 so that (x - 1) = ± √ ( - 4).
The roots are therefore x = 1 - √ ( - 4), and 1 + √ ( - 4),
These roots which are a combination of a real number and an imaginary number are called complex numbers.
The symbol i (j in electical work) is used to represent √ - 1. Therefore √ ( - 4) = 2i. The number i, or 1i , or xi are
called purely imaginary numbers.
The complex number solution of the above equation = and 1 + 2i and 1 - 2i,
Powers of complex are identified below
| i 1 = | +i | | i - 1 = | - i |
| i 2 = | - 1 | | i - 2 = | - 1 |
| i 3 = | - i | | i - 3 = | +i |
| i 4 = | +1 | | i - 4 = | - 1 |
| ... | ... | | i... | ... |
| i 5 = | +i | | i - 5 = | - i |
etc .
For two complex numbers (a 1 + ib 1) & (a 2 +ib 2)to
be equal it can be easily proved that a 1 must equal a 2, and b 1 must equal b 2
Complex numbers are conveniently represented using an argand diagrams as shown below.
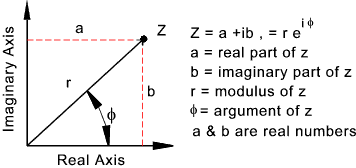
Complex numbers can be manipulated using the Cartesian system as follows;
z = a + i b
z 1 + z 2 = (a 1 + a 2) + i (b 1 + b 2)
z 1 - z 2 = (a 1 + a 2) - i (b 1 + b 2)
z 1 . z 2 = (a 1 . a 2 - b 1 .b 2) + i (a 1 . b 2 + a 2 .b a)
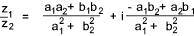
a2 + a2 = r2 = (a +ib) (a - ib)
Complex numbers can be manipulated using the polar co - ordinate system as follows;
z = a + i b = r (cos φ + i. sin φ )
r = √(a2 + b2 ),
φ = arctan (b/a) = tan - 1 (b/a)
sin φ = b/r, cos φ = a/r, tan φ = b/a
z 1. z 2 = r 1.r 2 [cos (φ 1 + φ 2 ) + i (sin (φ 1 + φ 2 ) ]
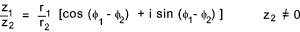
z n = r n [cos (n φ) + i sin (n φ) ] z > 0 , Integer
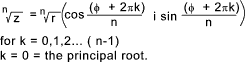
e i φ = cos ( φ) + i sin ( φ ) Eulers formula
i φ =ln [ (cos ( φ) + i sin ( φ ) ]
e - i φ = cos ( φ) - i sin ( φ ) = 1/ [ cos ( φ) + i sin ( φ ) ]
|