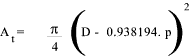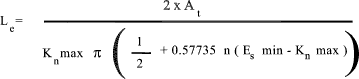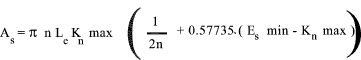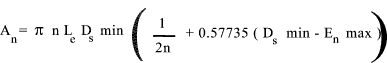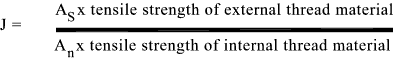Introduction
The critical areas of stress of mating screw threads are
- The effective cross section area, or tensile area, of the external thread.
- The shear area of the external thread which depends upon minor diameter of the tapped hole
- The shear area of the internal thread which depends on the major diameter of the external thread
|
The allowable stresses and screw end force and the method of applying the force in the calculation
of the tensile stress are not considered on this page but are addressed on this site by tables
and more importantly referenced links
If a screw threaded fastener is to fail it is preferable that the screw fails rather than the internal
or external thread strips. The length of the screw engagement should therefore be sufficient to carry
the full load necessary to break the screw without the threads stripping.
The size of a screwed fastener is first established by calculating the tensile
load to be withstood by the screw and selecting a suitable screw to withstand the tensile load
with the appropriate factor of safety or preload. If the joint is fixed using
a nut and bolt then assuming the nut is selected from the same
grade as the bolt there is little need to size the nut. The fastener manufacture
sizes the length of the nut to ensure the screw will fail before the nut. If the screw fastens
into a tapped hole then a check of the depth of thread engagement is required.
Generally for female and male threads of the same material with, the female thread is stronger
than the male thread in shear for the same length of engagement
The following rules of thumb are suggested for arriving at reasonable lengths of thread for steel screws used with screwed holes in weaker materials.
For steel a length of thread engagement of at least 1 x Nominal dia's of the thread
For Cast Iron or brass or bronze the thread engagement should be at least 1,5 x Nominal dia's of the thread
For Aluminium , zinc or plastices the thread engagement should be at least 2 x Nominal dia's of the thread
However for a quality safe connection, when the tapped material has a significantly lower ultimate tensile strength than the screw material,
- to ensure the screw will fail in tension before the female, it is preferable to use suitably rated nuts or engineered thread inserts.
For some notes on thread Inserts ref. Thread Inserts
Important Note:
Various studies on thread loading have established that
the shear stress is not evenly distributed across the threads. The first thread withstanding the load
is the highest stressed and the next one is much less stressed and so on... . If the thread materials were
very hard and did not yield the first thread could be withstanding nearly all
the load. However because of material yielding there is some distribution
of the load. A study (see link 2 below) has established that for a typical grade 8 nut the percentage
of the load taken by consecutive threads are about 34%, 23%, 16%,11%,9%, 7% .... This effect can be alleviated
by using very accurate threads and by using ductile materials for the components. It has been established that,for carbon steel,
there is no increase in thread shear strength by having a thread engagement length in excess of the screw diameter.
It is normal practice to use a tapped hole depth of about 1,5 x nominal diameter - this allows at least 1 diameter of good thread engagement.
A very simple rule that can be applied for that vast majority of applications is that a thread length of 80% of the
screw diameter (standard nut height) is sufficient for ensuring that the screw will fail in tension before the female thread (nut) fails in
thread stripping (assuming the screw and nut are similar materials). Equations below indicate how to make adjustments if
the tapped metal (nut) strength is lower than the screw/bolt.
|
Stress Area formulae
D = Basic Diameter.
p = Screw Thread Pitch
Le = Length of Thread Engagement
A t = The screw thread tensile stress area
d p = Pitch circle diameter of thread
A ss =The thread shear area
The following formula for the Tensile Stress Area of the (male) screw
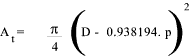
This is based on ISO 898 Part 1. see calculation below..
d p = Pitch circle diameter of thread
dp = (D - 0.64952.p )
The thread shear area = Ass
When the female and male threads are
the same material.
Ass = 0.5. π. dp. Le = 0.5 π (D - 0.64952.p ). Le
To ensure that the screw fails before the thread strips it is necessary the
the shear area is at least 2 times the tensile area. i.e
Le (min) = 2 . A t / [0.5 .π .(D - 0.64952.p )]
This assumes that the male and female thread materials have the same strength.
If the Female Material strength is lower i.e J as calculated below is greater than 1 then the length of engagement must be increased to prevent the female
thread stripping

If the value of J is greater than than 1 then the length of engagement must be increased
to at least
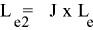
More Detailed Notes
The above formulae are sufficient to enable the tensile strength to be calculated
and to allow the depth of thread to be confirmed for a tapped hole
Following are equations to provide more accurate evaluation of the shear strength of
threads. These are equations derived from FED-STD-H28/2B, 1991 and Machinerys Handbook
eighteenth Edition. They strictly apply to UN thread series but if the relevent
metric screw thread dimensions are used they will give reasonable results. In practice
when the values are calculated the value for the screw shear strength is similar to the very
convenient formula provided above. These equations are only of theoretical value
Screw Shear Area Calculations
K nmax = Maximum minor diameter of internal thread.
E smin = Minimum pitch dia of external thread.
E nmax = Maximum pitch dia of internal thread.
D smin = Minimum major dia of external thread.
n = 1/p = threads per unit (mm)
Minimum Length Of Thread (Assuming male and female threads are materials of similar strength).
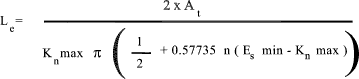
Shear Area For Screw
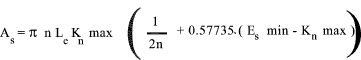
Shear Area For Female Thread
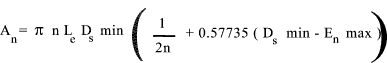
If material in which the female thread is tapped is significantly weaker
that the screw material then J must be evaluated.
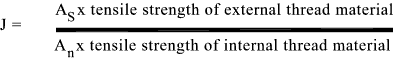
If the value of J is greater than than 1 then the length of engagement must be increased
to at least
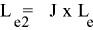
Stress area -ISO 898
Note: Short derivation of nominal stress area formula from info in BS EN ISO 898..
Some calculated Stress Areas for ISO Metric Threads..medium fit (6H / 6g)
The purpose of this table is to show the results of the above formula. It is
clear from this table that there is no major benefit in using the detailed formula
above. The approximate formula for the screw thread shear stress area
(A ss) is generally sufficiently accurate and there is no need to use
the more detailed formula for As. For sizes below M6 the formulas yield
very similar values. For sizes M6 and above the value for Ass provides a slightly more
conservative result (20% margin at M36)
I have obtained the thread dimensions on tables in Machinery's Handbook 27th ed. If you intend to
use this information please check it against a reliable source (ref disclaimer above)
All dimensions in mm
| Size |
|
M3 |
M4 |
M5 |
M6 |
M8 |
M10 |
M12 |
M14 |
M16 |
M20 |
M22 |
M24 |
M30 |
M36 |
| Basic Dia |
D (mm) |
3.00 |
4.00 |
5.00 |
6.00 |
8.00 |
10.00 |
12.00 |
14.00 |
16.00 |
20.00 |
22.00 |
24.00 |
30.00 |
36.00 |
| Pitch |
p |
0.50 |
0.70 |
0.80 |
1.00 |
1.25 |
1.50 |
1.75 |
2.00 |
2.00 |
2.50 |
2.50 |
3.00 |
3.50 |
4.00 |
| 1/p |
n |
2.0000 |
1.4286 |
1.2500 |
1.0000 |
0.8000 |
0.6667 |
0.5714 |
0.5000 |
0.5000 |
0.4000 |
0.4000 |
0.3333 |
0.2857 |
0.2500 |
| Stress Dia |
D s |
2.5309 |
3.3433 |
4.2494 |
5.0618 |
6.8273 |
8.5927 |
10.3582 |
12.1236 |
14.1236 |
17.6545 |
19.6545 |
21.1854 |
26.7163 |
32.2472 |
| Tensile Stress Area |
A t |
5.0308 |
8.7787 |
14.1825 |
20.1234 |
36.6085 |
57.9896 |
84.2665 |
115.4394 |
156.6684 |
244.7944 |
303.3993 |
352.5039 |
560.5872 |
816.7226 |
| Pitch circle dia. |
d p |
2.6752 |
3.5453 |
4.4804 |
5.3505 |
7.1881 |
9.0257 |
10.8633 |
12.7010 |
14.7010 |
18.3762 |
20.3762 |
22.0514 |
27.7267 |
33.4019 |
| Approximate Method |
| Shear Area/unit Length |
Ass/mm |
4.2023 |
5.5690 |
7.0378 |
8.4045 |
11.2910 |
14.1776 |
17.0641 |
19.9506 |
23.0922 |
28.8653 |
32.0069 |
34.6383 |
43.5530 |
52.4676 |
Shear Area
|
Assm
=2. At |
10.0616 |
17.5574 |
28.3650 |
40.2468 |
73.217 |
115.9792 |
168.533 |
230.8788 |
313.33568 |
489.5888 |
606.7986 |
705.078 |
1121.1744 |
1633.4452 |
Length of Thread
(Ass=2*At) |
Le =
Ass /A ss/mm |
2.3944 |
3.1527 |
4.0304 |
4.7887 |
6.4845 |
8.1805 |
9.8765 |
11.5725 |
13.5689 |
16.9612 |
18.9584 |
20.3534 |
25.7428 |
31.1324 |
| More Accurate Method |
| Max.Minor Dia (nut) |
Knmax |
2.5990 |
3.4220 |
4.3340 |
5.1530 |
6.9120 |
8.6760 |
10.4410 |
12.2100 |
14.2100 |
17.7440 |
19.7440 |
21.2520 |
26.7710 |
32.2700 |
| Min Pitch Dia (Screw) |
E smin |
2.5800 |
3.4330 |
4.3610 |
5.2120 |
7.0420 |
8.8620 |
10.6790 |
12.5030 |
14.5030 |
18.1640 |
20.1640 |
21.8030 |
27.4620 |
33.1180 |
| Max Pitch dia (Nut) |
E sub>nmax |
2.7750 |
3.6630 |
4.6050 |
5.5000 |
7.3480 |
9.2060 |
11.0630 |
12.9130 |
14.9130 |
18.6000 |
20.6000 |
22.3160 |
28.0070 |
33.7020 |
| Min Major dia (Screw) |
D smin |
2.8740 |
3.8380 |
4.8260 |
5.7940 |
7.7600 |
9.7320 |
11.7010 |
13.6820 |
15.6820 |
19.6230 |
21.6230 |
23.5770 |
29.5220 |
35.4650 |
| Shear Area/unit length (Screw) |
A s /mm |
3.9034 |
5.4728 |
7.0731 |
8.6458 |
12.1612 |
15.5796 |
18.9762 |
22.4239 |
26.0969 |
33.2791 |
37.0302 |
40.4623 |
51.6384 |
63.0982 |
| Shear Area /mm length (Nut) |
A n/mm |
5.5466 |
7.7691 |
9.9988 |
12.1909 |
16.8285 |
21.4769 |
26.1173 |
31.0335 |
35.5699 |
45.3881 |
50.0141 |
55.0098 |
69.5512 |
84.0601 |
Length of Thread
(As= 2*At) |
Le |
2.5777 |
3.2081 |
4.0103 |
4.6551 |
6.0206 |
7.4443 |
8.8813 |
10.2961 |
12.0067 |
14.7116 |
16.3866 |
17.4238 |
21.7120 |
25.8873 |
|