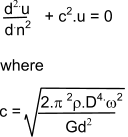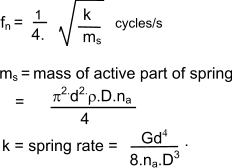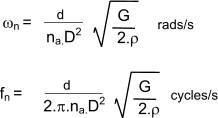If a spring which is subject to a vibratory motion which is close to its natural frequency the spring can start to surge.    This situation is very undesireable because the life of the spring can be reduced as excessive internal stresses can result.     The operating characteristics of the spring are also seriously affected.     For most springs subject to low frequency vibrations surging is not a problem.    However for high frequency vibrating applications it is necessary to to ensure, in the design stage, that the spring natural frequency is 15 to 20 or more times the maximum operating vibration frequency of the spring.

Note: metres (m) have been shown as the units of length in all of the variables above for consistency.   In most practical calculations milli-metres will be more convenient.

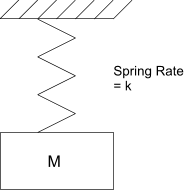
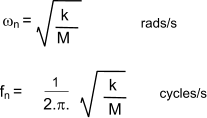
Generally springs are designed to have a deflection proportional to the applied load (or torque -for torsion springs).   The "Spring Rate" is the Load per unit deflection.... Rate (N/mm) = F(N) / δ _e(deflection=mm)

Consider a mass M supported on a weightless spring with a spring rate k is illustrated below

This system has a natural frequency as shown below.

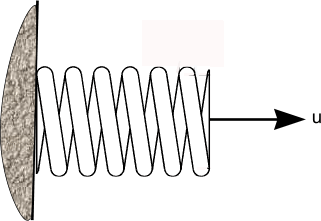
This frequency is the lowest natural frequency and is the most important natural frequency.     The spring , however not weightless and thus it has vibration characteristics of its own.    Vibration effects within the spring and the associated frequencies are found by examinging a small element of the spring in harmonic motion.

For more detailed notes refer to webpage Simple Harmonic Motion

Consider a spring below subject to a vibration amplitude u at a circular frequency ω

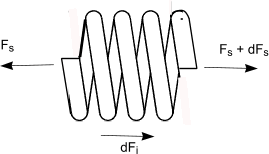
Consider a small element of the spring comprising dn coils.     The density of the spring material is ρ and the length of the wire in the element is π.D.dn.     If the wire diameter is d then the element has a mass

For a vibration amplitude u at a circular frequency ω and at any axial location from coil n = 0 to coil n = n_a the inertial force amplitude is as follows.

The spring rate k for a helical spring is derived on webpage Helical Springs as ..

In practice the term (1 + 0,5/C²) which approximates to 1 can be ignored

For the purpose of this analysis this is transformed to

This equation represents the force for n_a active coils .

The spring force amplitude per active coil resulting from a spring deflection per coil du/dn is

Equating the forces on the spring element to zero the equation below is derived.

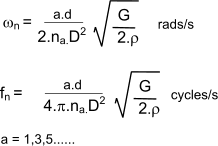
This equation is solved using the equation.

u = A sin(c.n) + B cos(c.n)

A and B are arbitrary constants.
For a spring fixed at one end and free at the other the boundary condition occurs at

u = 0 occurs at coil 0
and the condition du/dn = 0 is applied at n = n_a

Resulting in the solution B = 0 and cos(c.n_a) = 0 from which

c.n_a = a.π / 2               ( a= 1,3,5 .....)

This results in a set of natural(surge)frequencies as follows..

For the important fundamental natural frequency, this can be simplified to..

Import Note : The above analysis relates to a spring with one end against a flat surface and the other end free.     The fixed.. fixed case i.e a spring located between and in full contact with two plates results in similar solutions where a = 2, 4, 6......This is also applicable to a spring with one end fixed and against a plate and the other end driven with a sin-wave motion.     The fundamental surge frequency resulting from these scenarios are