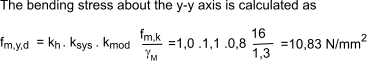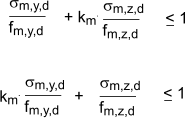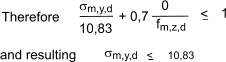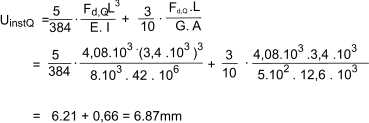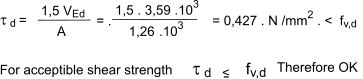To Design the timber floor joists for a domestic dwelling using timber of strength clss C16 based on the following data

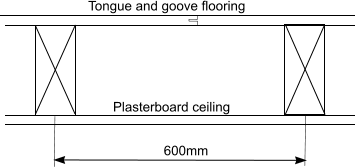
Floor width , b = 3,6m and floor span L is 3,4m
Joists are spaced at 600 mm centres
Flooring is tongue and groove of thickness 21mm and self weight of 0,1 kN /m²
Ceiling is plasterboard with a self weight of 0,2 kN/m²
Bearing length = 100mm
Area of floor supported by each joist = Joint pitch . floor span A = 0,6  .  3,4 = 2,04 m²

Design Actions

Specific permanent action, g_k
Tongue & grove boarding = 0.10 kN /m²
Ceiling = 0.20 kN /m²
Joists (say) = 0.10 kN /m²....
{ Each m² includes about 2m of joist (assume 63mm x 200 mm with a csa of 12,6 mm² ) this has a volume of about 25,2m^-3m³ which at an average density of 370 kg/m³ weighs approx 9 kg.
The specific weight of the joists per m² is therefore about 0,093kN/m² }

Total characteristic permanent action = G_k 0,1  +  0,2  +  0,1  =   0,4 kN /m²

Specific variable action, q_k
Imposed floor load for domestic dwelling (Eur. Intro _Imposed loads) is 2,0 kN /m^-2

Design Load on the joists is

F_d = γ_G.G_k + γ_Q.Q_k = γ_G.g_k . A + γ_Q.q_k. A
= 1,3  .  0,4  .  2,04  +   1,5  . 2,0   .  2.04   =  7,181 kN

Characteristic Properties of timber of class C16. ( N/mm² )

Bending

Assuming that the average moisture content of the timber joists does not exceed 20 per cent during the life of the structure, design the joists for service class 2. Service Class
Also as the joists are required to carry permanent and variable (imposed) actions, the critical load duration class is �medium-term� . Design strength values
Therefore k_mod = 0,8 and γ_GM (for ultimate limit states) = 1,3 Design Strength Values
As the joists form part of a load sharing system the design strengths can be multiplied by a load sharing factor, k_sys = 1,1 Design Strength Values

As the (assumed) beam is in bending and is over 150mm depth a value of k_h = 1,0 is used

If members are not to fail in bending, the following conditions should be satisfied:

It is clear from   
Sawn timber geometry A 63 mm � 200 mm joist (as assumed initially ) would be suitable
Wy = 420 � 10³ mm³, Iy = 42 � 10⁶ mm⁴, A = 12.6 � 10³ mm².

Deflections

Note simple equation used in this section are obtained from the following pages
Stress and strain
Shear stress

Instantaneous deflection due to permanent actions u_instG

The Partial factor γ_M for serviceability limit states = 1,0
Also the factored permanent load G = γ_G. G_k = 1,0 x 0,40 = 4,0kN/m² .

The factored permanent load per joist F_d,G =

F_d,G = total load x joint spacing x span length = 0,4 x 0,6 x 3,4 = 0,82 kN

The instantaneos deflection due to permanent actions u_instG results from

u_instG = bending deflection + shear deflection.

The instantaneous deflection due to variable actions u_instQ results from
The Partial factor γ_M for serviceability limit states = 1,0
Also the factored permanent load Q = γ_Q. Q_k = 1,0 x 2,0 = 2,00 kN/m² .

The factored permanent load per joist F_d,Q =

F_d,Q = total load x joint spacing x span length = 2,0 x 0,6 x 3,4 = 4,08 kN

Final deflection due to permanent actions reference... Deflections
For solid timber members subject to class 2 loading K_def = 0,8 .    the final deflection due to permanent actions u_fin,G is given by

u_fin,G = u_inst,G ( 1+ k_def) = 1,13 *1,8 = 2,034mm

Final deflection due to variable actions reference ...Deflections, reference Factor values
For solid timber members subject to class 2 loading K_def = 0,8 . and for the variable action factor ψ₂ = 0,3     the final deflection due to permanent actions u_fin,Q is given by

u_fin,Q = u_inst,Q ( 1+ ψ₂ . k_def) = 6.87 * (1 + (0,3.),8) = 8,51mm

Checking the final deflection

u_fin = u_fin,G + u_fin,Q
= 2,034 + 8,51 = 10,544 mm
The permissible final deflections assuming the floor supports brittle finishes w_fin =
w_fin= 1/250 .span = (1/250).3400mm = 13,6mm
13,6mm > 10,544mm ..therefore deflection is acceptable.

Vibration

Assuming that f1 > 8 Hz it is necessary to check that

W/F     ≤    a            and        ν    b^{(f1.ζ -1 )}

k_strut = 1,0
(EI)_b = 8 .10³ .(1000.21³ / 12) = 6,18 .10⁹ Nmm² /m
Joist spacing s = 600 mm

Hence k_dist =

Hence k_dist = k_strut[0,38 -0,08 ln[14(EI)_b/s⁴ ]     ≥     0,30
= 1,0.[0,38 -0,08 ln[14 . 6,18 . 10⁹/600⁴ ] = 0,33
L_eq = 3400mm
k_amp = 1,05
(EI)_joist = 8 .10³ .(63.200³ / 12) = 3,36 .10¹¹ Nmm² /m

Therefore the maximum deflection caused by a concentrated static force F = 1,0, w, is

Check impulse velocity

Floor width, b = 3.4 m and floor span, l = 3.6 m.
I_y is the second moment of area of the joist (ignore tongue and groove boarding unless a specific shear calculation at the interface of joist and board is made):

I_y = 42 . 10⁶ mm⁴ = 42 . 10^-6 m⁴

E_0,mean = 8 000 N / mm² = 8 . 10⁹ N / m²

(EI)_L = E_0,meanI_y / joist spacing

= 8 . 10⁹. 42 . 10^-6 / 0,6 = 5,6 . 10⁵ Nm² /m

Mass due to permanent actions per unit area, m, is

m = permanent action / gravitational constant
= 0,40 � 10³ / 9.81 = 40,8 kg /m²

The fundamental frequency of vibration, f₁, is

The number of first order modes n₄₀ is

The unit input velocity is

Assume the damping coefficient ξ = 0,002 form since a ( = 0,82mm) < 1 is given by

b = 180 -60.a = 180 - 60 . 0,82 = 131

Hence Permissible floor velocity =

Lateral Buckling

It is not necessary to check for lateral buckling because the beams are all supported along their length by the upper tongue and groove boards.

Shear

Reference... Shear

The design shear strength is

The maximum shear force is

Design shear stress at the neutral axis is

Bearing

reference Compression

The bearing design force is

F_90,d = F_d/2 = 7.181 . 10³ /2 = 3,59 . 10³ N

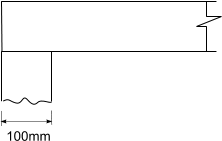
The design bearing stress

Assuming that the floor joists are supported on 100m wide wallls as shown above the bearing stress resulting is calculated by

The design bearing strength

The design compressive strength perpendiculr to the grain f_c,90,d is calculated as

a = 0 , L₁ = 0 Therefore k_c,90 = 1