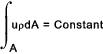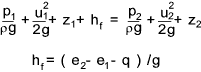This webpage includes various notes relating to fluid flow and flowpaths and flow patterns at a very basic level.

When considering the flow of a fluid it is often convenient to consider the flow as a number of imaginary curves along which individual particles of fluid flow.  These lines are called streamlines or flowlines.  fluid particles only flow along the streamlines and no particles cross the lines.  A number of streamlines bundled together is termed a streamtube.  he boundary of a streamtube is composed of streamlines and by definition of a streamline fluid can only enter and leave a streamtube at its ends.

The flow of fluid is always clearly three dimensional.  However when considering flow problems it is generally more convenient and practical to consider flow as two dimensional or one dimensional.   When considering flow along a pipe it is convenient, and practical to consider the flow along the centreline of the pipe run, that is as one dimensional flow.  The pressure loss, and variations of velocity etc are along the pipe centre line.  Macro pipe flow is more nearly two dimensional because the fluid velocity varies across the diameter with zero velocity at the pipe wall and the maximum velocity at the pipe centre.  This problem is overcome in pipe flow calculations by assuming the flow velocity as the mean velocity.  Water flow over a long weir is in reality three dimensional at the ends but can be considered as two dimensional flow with corrections for the ends.

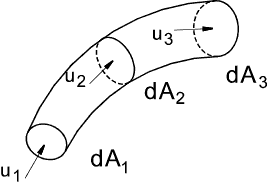
Internal flow is flow within the boundary walls.   Types of internal flow include pipe flow, channel flow, airflow in ducts.   This type of flow is controlled using valves, fans , pumps.

External flow is flow outside of a boundary or body.  Examples of this type of flow include flow over aircraft wings, flow around immersed bodies, air flow around buildings and airflow around cars.

A very important separation of flow types relates to the velocity of the flowing fluid.   Fluid flow at low velocities is smooth with the fluid particles moving in straight lines along the direction of flow.  This type of flow is called laminar flow.  The majority of flows in practice are turbulent with no uniform motion at the local level but an average velocity in the direction of flow.  By using experimentally derived results Osborne Reynold (Manchester UK ) determined flow ranges separating the flow types for the majority of fluids.   A dimensionless quantity was identified ( vρl/μ ) called Reynolds number. If the conditions and properties of flowing fluid are such the relevant Reynolds number is less than 2000 the flow will be laminar.  If the relevant Reynolds number is greater than 4000 then the flow will be turbulent.  Flows in the transition region between are termed critical and may be laminar or turbulent or a bit of each.   For pipe flow v is the mean velocity, l is the pipe diameter ρ is the fluid density and μ is the viscosity.  This differentiation of flow occurs if the fluid is a liquid or a gas.

Another classification of flow is steady flow which is defined as the type of flow in which the various parameters at any point do not change with time.  Flow which changes with time is unsteady or non-steady flow.  Real flows are generally the latter type but in completing flow assessments it is often more practical to assume steady flow conditions.

Viscous Flows are flows whose flow patterns are dominated by the viscous properties of the fluid.  This occurs in fluids where the velocity gradients are large e.g. within pipes close to the walls of the pipe.  When the viscous properties are not dominant the flow is defined as inviscid flow.  This type of flow is prevelant in the centre region of flowing pipes and in gas flows.

The majority of liquids are virtually incompressible under the majority of operating conditions from open channels to high pressure hydraulic systems.  Flow involving liquids are generally considered to be incompressible flows.  It is only during exceptional flow events such as water hammer when liquids do not behave as incompressible fluids.   Gases are compressible fluids and flow involving gases are often compressible flows .   The effects of variation of density along the flow paths require special consideration when determining the operationing parameters such as the head loss along the flow path.  For many gaseous flows the velocities are low and the pressure drops are also low such that they can be considered as compressible flows.

It is often important to consider the flow velocity relevant to the speed of sound and the Mach number (Fluid velocity/ Fluid sonic velocity) is important.  Fluid velocities are generally limited such that the mach number does not exceed 1.

The continuity equation is really a mathematical version of the principle of the conservation of mass as applied to fluid flow.   If a region is defined in a fluid and steady flow conditions apply ..then.

The rate at which mass enters the region = The rate at which mass leaves the region

Considering a stream tube as shown below whose section is so small that the velocity u and the density ρ do not vary across it.
The flow across the section = udA and the mass flow across the section is uρdA.

There is not mass accumulation within the stream tube under steady flow conditions therefore

u ₁ρdA ₁   =  u ₂ρdA ₂  =  u ₃ρdA ₃  =  Constant

Considering a cross section of flow i.e. a pipe length with cross section A consisting entirely of stream tubes the equation above can be integrated as follows

The local velocity u is assumed to be normal to the local cross section and the density and velocity are constant over the entire local section then.

uρA = Constant

For fluids of constant density (incompressible fluids -liquids) with average flow u this reduces to

uA = Constant = Q

That is, under the conditions specified, when the area increases the velocity reduces and vice versa

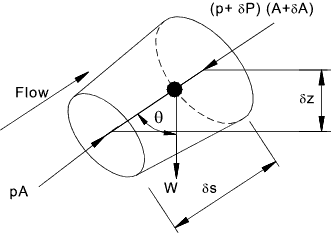
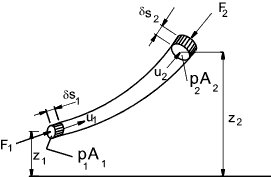
The equation is an expression of the conservation of energy.   Initially the only forces considered are gravity, pressure and inertial forces.  The viscosity forces are assumed to be neglible.   The fluid is assumed to be a perfect inviscid fluid under steady flow conditions.

The velocity of a fluid varies and this is associated with forces which may be linked using Newtons first law

Newtons First law ...Every body continues in a state of rest or of uniform rectilinear motion unless acted upon by a force

The relationships between the changes can be analysed using Newtons second law..

Newtons Second law ...The time rate of change of linear momentum of a body is proportional to the unbalanced force acting on the body and occurs in the direction in which the force acts. i.e  Force = Mass.Acceleration.

Applying Newtons first law to a small element of fluid within a single streamline of small cross section as shown below.   The ends of the streamline are assumed normal to the centre line of the streamline .   Considering the forces of pressure and gravity around the element and ignoring all other forces (viscosity , surface tension, magnetism, nuclear etc).

Upstream the pressure is p and downstream the pressure is (p + δp).   δp may be negative.  The forces at the side of the element vary but it will be assumed that the mean pressure is (p +kδp ) with k being some value less than one.   Taking forces in the direction of flow and noting that the hydrostatic forces on the sides mean = (p +kδp ) are acting on the area δA - all other side forces are perpendicular to the axis and are ignored.   The weight of the element = ρgAδs

Resultant Force = pA - (p + δp)(A+ δA ) + (p + kδp)δA - ρgAδs cos θ

ignoring second order of small quantities...

Resultant Force = Aδp - ρgAδs cos θ

The mass of the element is constant and therefore the resultant force must be equal to the mass times acceleration of the element in the direction of the force du/dt .

ρAδs (du/dt) = Aδp - ρgAδs cos θ

Now ( δs cos θ) = δz where z represents height above a horizonatal datum level.
Dividing throughout by ρAδs and taking the limit δs -> 0

Consider a particle moving along a steady flow streamline for which the velocity changes as the particle moves along the streamline e.g the velocity increases as the area of the streamline reduces.   δu = [ du/ds ]δs.  Therefore in the limit δt -> 0 the local acceleration with respect to time is

Therefore if (du/dt) is replaced by u(du/ds) the following equation results...

For fluids of constant density the equation can be integrated with respect to s as follows.

The resulting equation (in both forms) is known as Bernouli's equation and is probably the most widely used in fluids and hydraulics and explains many of the phenomena encountered in these areas of engineering.  In the second form each term has the energy per unit weight ρg and has units [ML² /T²] / [ML /T²] = [L].  The terms are identified as pressure head, velocity head, and gravity head.

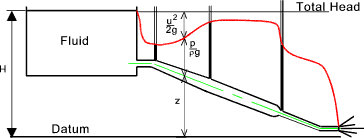
The figure below shows a hypothetical fluid system taking no account of friction losses in the pipe line.   The gauge points show the pressure head at the connection point.  The differences in level between the gauge level (red line) and the tank level represents the kinetic head.

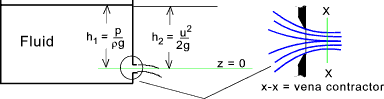
The figure below illustrates the condition of a perfect fluid flowing out of reservoir through a sharp edged orifice.   The fluid flows out as a free jet.   The datum z is assumed to be at the centre line of the orifice.

At the inlet the total energy is equal to the hydrostatic head of the fluid h₁ = p /( ρg ). At the exit from the orifice at the point of maximum velocity (vena contracta) the head is virtually = to the velocity head h₂ = u² /(2g).   As h₁ = h₂ it is clear that the maximum velocity of the fluid flowing out of the tank is

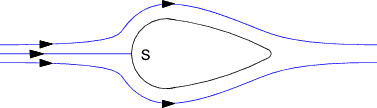
Considering bluff object located in a flowing fluid.

The off line flowstreams generally divert round the object as shown but the centre flow stream is such that at the surface of the object the velocity in the direction of the flowsteam = zero.  This is called a stagnation point.

Now by bernoulli's equation the (pressure + velocity + head) energy is constant along the flowstream and consequently at the stagnation point the pressure is increased from p to p + (1/2) ρ u².as the velocity energy is converted to pressure energy.  For a constant density fluid the value of ( p + (1/2) ρ u² ) is known as the stagnation pressure of the streamline.

A manometer connected to point S would indicate the stagnation pressure (p /ρg +u ² /2g) and therefore if the static head (p /ρg) was known then by subtraction the velocity head and hence the velocity could easily be calculated.  The is how the pitot tube meter works ref. Pitot tube meter .

Bernoulli's equation is fundamental to fluid flow analysis but it is subject to certain important simplifications.   It assumes the fluid is inviscid and incompressible and that the flows are steady and relationships have been derived using newtons laws based on flows alone a single streamline.  When considering the flow of real fluids it is necessary to include for energy losses and energy gains.  The first law of thermodynamics is reviewed in outline on webpage Laws of Thermodynamics and basically identifies the transfer of energy over a complete cycle for a system as follows

Δ Q = ΔE + ΔW

Δ Q is the increase of energy supplied to a system, Δ E is the increase in the total energy of a system and Δ W is the mechanical work done by the system.  In fluids the processes are flow processes and the first law is expressed in the form of the "steady flow energy equation as shown below..

q = net heat transferred to fluid per unit mass =
the net work done by the fluid [p₂ / ρ₂   -   p₁ / ρ₁   +   w ]   +  
the net increase in the kinetic energy (u ₂ ² /2 - u ₁ ² /2 )  +  
the net increase in the gravitational energy (z₂ g - z₁ g )   +  
the net increase in the internal energy (e₁ - e₂).

This law applies to fluids with steady and continuous flows and the conditions at the inlet and outlet points (section 1) and (section 2), heat and work energy transfer rates are constant.

This very general law applies to all flowing fluids.  When applied to liquids under normal flow conditions e.g in pipes and channels, with no heat transfer and no mechanical work being performed the steady flow energy equation can be reduced to.

h _f is the energy lost as a result of friction and is dissipated in increasing the internal energy of the fluid (e₂ - e₁ ) and as heat lost to the environment (q)

Bernoulli's theorem indicates that if the hydrostatic head (p/ρg +z) decreases then the fluid accelerates. Consider a streamtube (or pipe) as shown below.

Bernoulli's formula can be rewritten as

From the basic laws of motion ref. Dynamics

u₁ is the initial velocity and u₁ is the final velocity, s = distance , and a = acceleration.

Therefore

The left hand side of this equation is the drop in the piezometric head - ( the head measured by a manometer type gauge).  If the slope of this decrease in piezometric head is i then the head drop is iδs ..s being the distance along the streamtube or pipe.. Therefore....

According to Newtons second law acceleration = force/unit mass.

Form the intitial notes on bernoulli's principle above ref Bernoulli's Equation

This equation relates to forces in the direction of the axis of motion.  For an incompressible fluid the piezometric head gradient ( i ) in any direction produces a corresponding force per unit mass in that direction equal to ( ig ).  Assuming negligible viscous friction this is the only force acting on the fluid and can be equated to the corresponding fluid acceleration in that direction.